Indice del artículo
ECUACIONES , INECUACIONES Y SISTEMAS.
Examen2
EXAMEN 3
EXAMEN 4
EXAMEN 5
EXAMEN 6
Todas las páginas

Título de la materia:	Matemáticas orientadas a las Enseñanzas Académicas
Nivel:	ESO 4	Opción:	F
Nombre:		Grupo:
Evaluación:		N.º:
Calificación:		Fecha:

 

Ejercicio nº 1.-

 

Resuelve:

 

 

 

Solución:

 

 

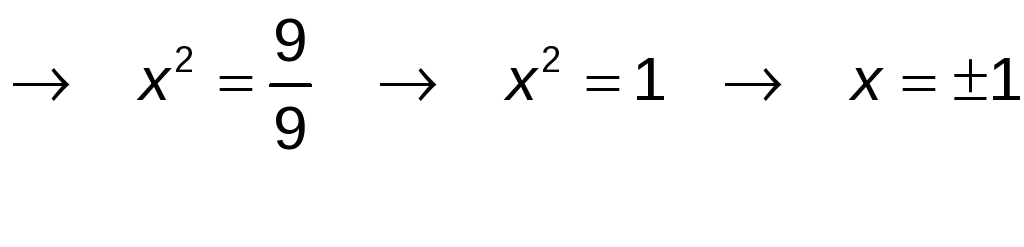
Las soluciones son x₁= 1 y x₂=−1.

 

b) Ecuación bicuadrada; hacemos x²= z y obtenemos:

 

 

 

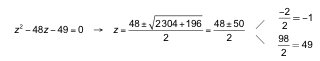
Las soluciones son x₁= 7 y x₂= −7.

 

 

 

 

Ejercicio nº 2.-

 

Resuelve:

 

 

 

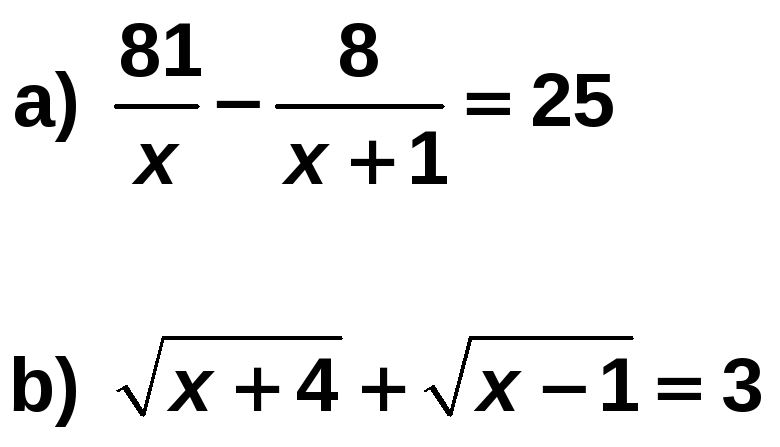
Solución:

 

a) Multiplicamos ambos miembros por x (x + 1):

 

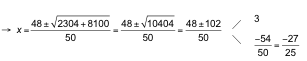
Comprobamos si son, o no, solución en la ecuación inicial:

 

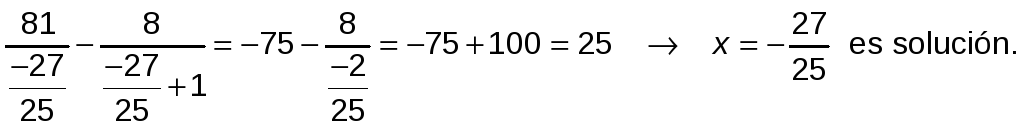
Elevamos ambos miembros al cuadrado:

Volvemos a elevar al cuadrado:

Comprobamos si es, o no, solución:

 

 

 

Ejercicio nº 3.-

 

 

 

 

Solución:

 

Tenemos un producto de factores igualado a 0, luego se ha de cumplir:

x = 0

 

 

 

 

 

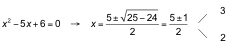
Ejercicio nº 4.-

 

Resuelve las siguientes ecuaciones:

 

 

b) 2log x = log (15 ‒ 2x)

 

 

Solución:

 

→ 2^3x+ 2^6x= 4 160

 

Hacemos un cambio de variable: t = 2^3x

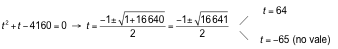
64 = 2^3x→ 2⁶= 2^3x→ x = 2

 

b) 2log x = log (15 ‒ 2x) → log x²= log (15 ‒ 2x) → x²= 15 ‒ 2x →

 

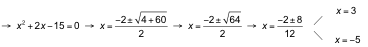
La solución válida es x = 3, puesto que, log (‒5) no existe.

 

 

 

 

Ejercicio nº 5.-

 

en reformar la casa, el 10% de la cantidad inicial en ropa y el resto, 260 €, los ahorró. ¿Cuánto dinero heredó?

 

 

Solución:

 

x = "dinero heredado"

 

La ecuación que resuelve el problema será:

Multiplicamos ambos miembros por 30:

 

 

 

 

Ejercicio nº 6.-

 

Resuelve por el método que consideres más apropiado y comprueba la solución obtenida en el siguiente sistema:

 

 

 

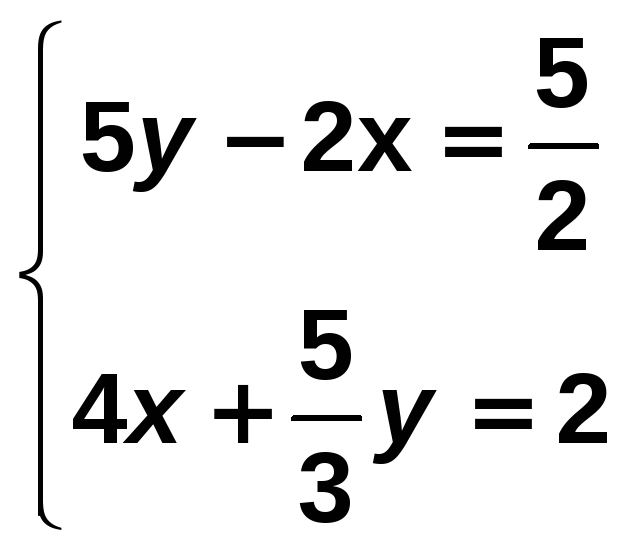
Solución:

 

Utilizamos el método de reducción en y ; para ello multiplicamos la 2ª ecuación por −3:

 

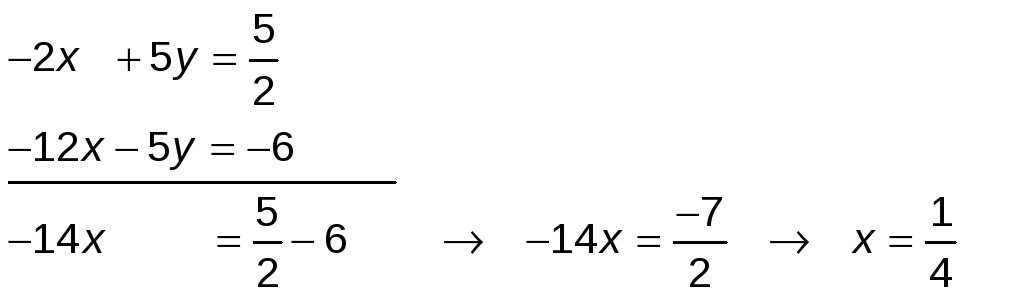
Calculamos y sustituimos el valor de x en la 1ª ecuación:

 

 

Comprobamos la solución:

 

 

 

 

 

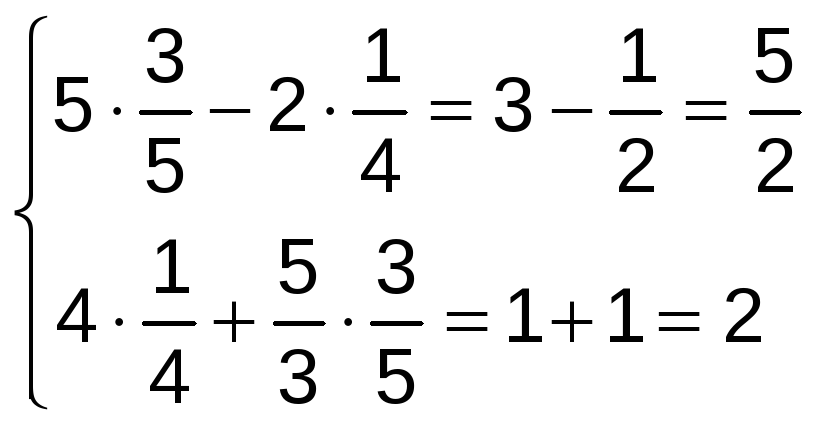
Ejercicio nº 7.-

 

Resuelve:

 

 

 

Solución:

 

 

Aplicamos el método de igualación:

 

Elevamos al cuadrado los dos miembros de la última igualdad:

 

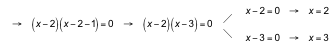
Comprobamos las soluciones sobre el sistema:

 

 

 

 

 

 

Ejercicio nº 8.-

 

Pablo compró un equipo de música y un reproductor de DVD por 870 €. Después de algún tiempo, los vende por 770,50 €. Con el equipo de música perdió el 10% de su valor y con el reproductor de DVD el 15%. ¿Cuánto le costó cada uno?

 

 

Solución:

 

Llamamos:

x = “precio inicial del equipo de música”

y = “precio inicial del reproductor de DVD”

Aplicamos el método de sustitución:

x = 870 − y

0,90 (870 − y) + 0,85y = 770,50 → 783 − 0,90y + 0,85y = 770,50 → −0,05y = −12,5 → → y = 250

x = 870 − y → x = 870 − 250 = 620

El equipo de música costó 620 € y el reproductor de DVD 250 €.

 

 

 

 

Ejercicio nº 9.-

 

a) Resuelve gráficamente la inecuación, expresando la solución en forma de intervalo:

 

b) Halla el conjunto de soluciones de la inecuación:

 

x² + 3x ‒ 6 > 8 ‒ 2x

 

 

Solución:

 

 

 

 

 

 

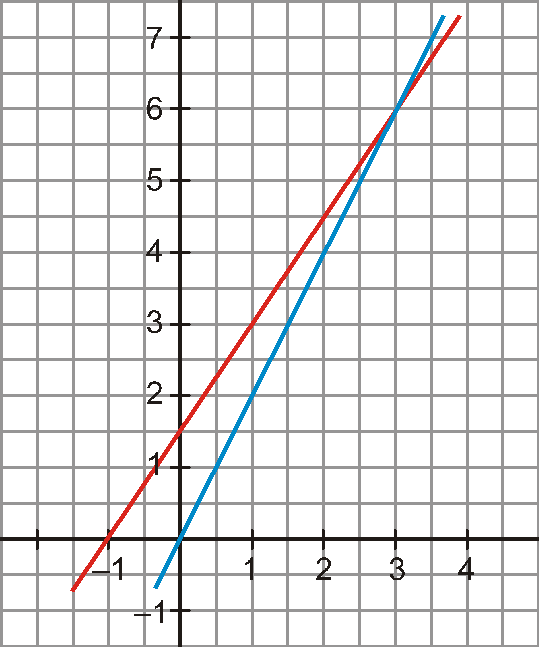
b) x²+ 3x ‒ 6 > 8 ‒ 2x → x²+ 5x ‒ 14 > 0

 

Resolvemos la ecuación x²+ 5x ‒ 14 = 0:

 

 

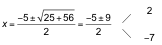
Estudiamos el signo de x²+ 5x − 14 según los valores que damos a x.

 

Los valores −7 y 2 dividen la recta real en tres partes, en cada una de las cuales estudiaremos el signo de x²+ 5x − 14.

 

 

 

 

 

 

 

 

Ejercicio nº 10.-

 

Resuelve el siguiente sistema de inecuaciones:

 

 

 

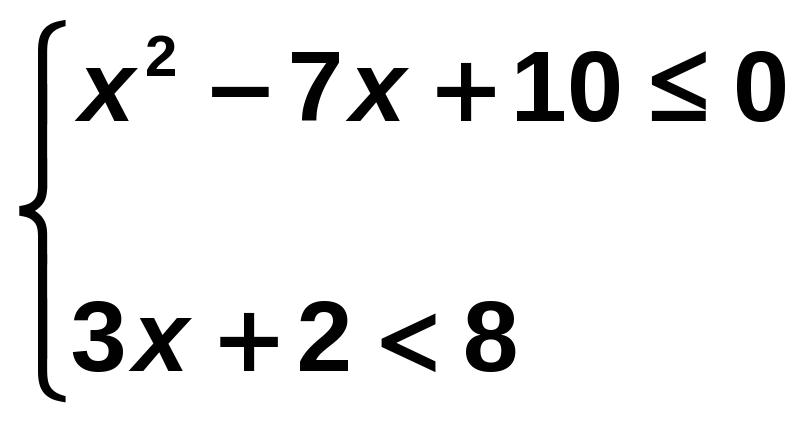
Solución:

 

Resolvemos independientemente cada inecuación y buscamos las soluciones comunes:

 

 

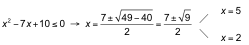
La solución de esta inecuación es [2, 5].

 

3x + 2 < 8 → 3x < 6 → x < 2

 

Este sistema de inecuación no tiene solución.

 

 

 

 

 

Ejercicio nº 11.-

 

En un triángulo isósceles el lado desigual es la mitad de los lados iguales.

 

a) Para que el perímetro no supere los 30 cm, ¿qué puedes deducir de la longitud de los lados?

 

b) ¿Y si además buscamos un perímetro al menos de 15 cm?

 

 

Solución:

 

 

 

 

Los lados iguales no deben superar los 12 cm y el lado desigual ha de ser menor o igual

Luego uniendo ambos apartados llegamos a la siguiente conclusión:

− Los lados iguales, x, miden como mínimo 6 cm y como máximo 12 cm (6 ≤ x ≤ 12).

 

 

 

 

Ejercicio nº 12.-

 

Calcula los valores que ha de tomar k para que la ecuación x² − 6x + k = 0 tenga:

 

a) Dos soluciones iguales.

b) Dos soluciones que no sean números reales.

 

 

Solución:

 

a) Tendrá dos soluciones iguales cuando b²− 4ac = 0, es decir,

(−6)²− 4k = 0 → 36 − 4k = 0 → k = 9

 

b) Que las soluciones no sean números reales equivale a decir que la ecuación no tenga solución en el campo de los números reales; esto ocurre cuando b²− 4ac < 0.

36 − 4k < 0 → 36 < 4k → k > 9

 

 

 

 

Ejercicio nº 13.-

 

Un tractor sube un camino montañoso a 30 km/h y lo baja a 50 km/h. Calcula la velocidad media del recorrido.

 

 

Solución:

 

Hacemos un cuadro para organizar los datos y ayudarnos en el planteamiento del problema.

 

	DISTANCIA (km)	VELOCIDAD	TIEMPO (h)
SUBIDA	d	30 km/h
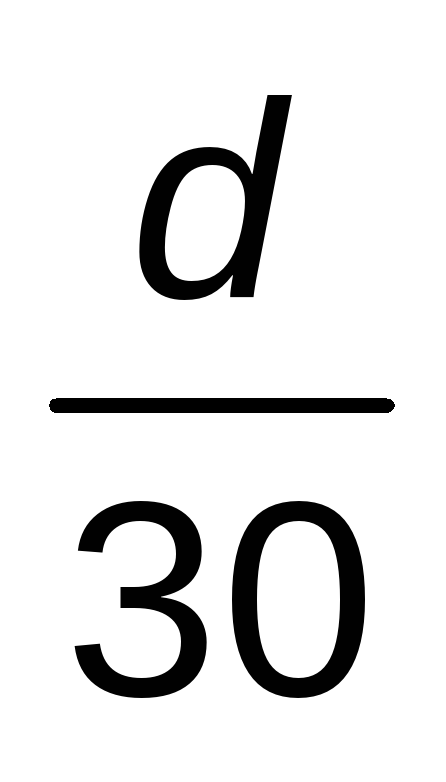
BAJADA	d	50 km/h
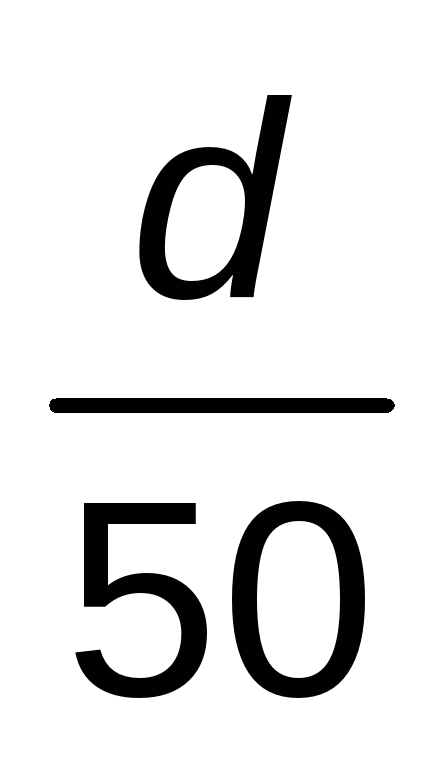
TOTAL RECORRIDO	2d	x

 

 

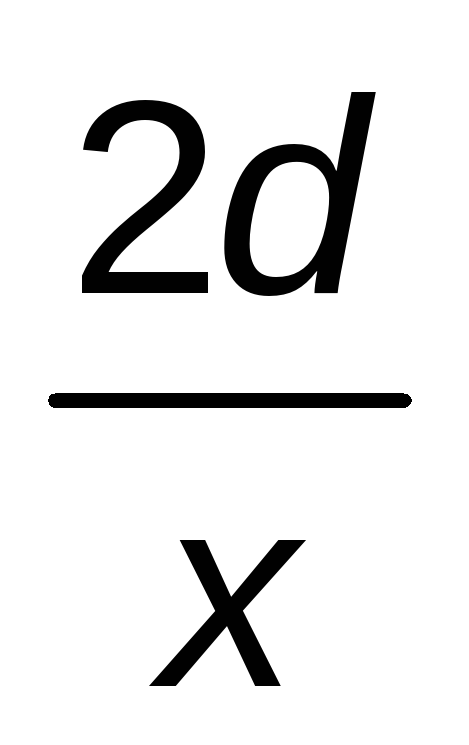
Por tanto:

 

 

Dividiendo entre d:

 

 

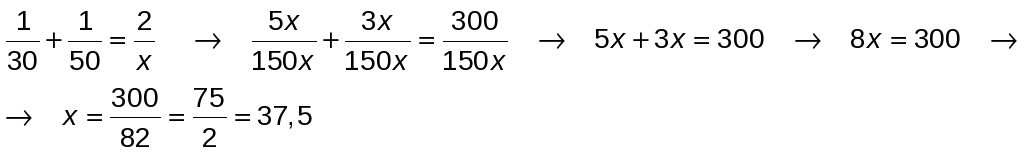
La velocidad media del recorrido ha sido de 37,5 km/h.