| Indice del artículo |
|---|
| ECUACIONES , INECUACIONES Y SISTEMAS. |
| Examen2 |
| EXAMEN 3 |
| EXAMEN 4 |
| EXAMEN 5 |
| EXAMEN 6 |
| Todas las páginas |
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | A |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve las ecuaciones:
![]()
Solución:
a) Sabemos que si a2 = b2, entonces, o bien a = b o bien a = −b.
En este caso:
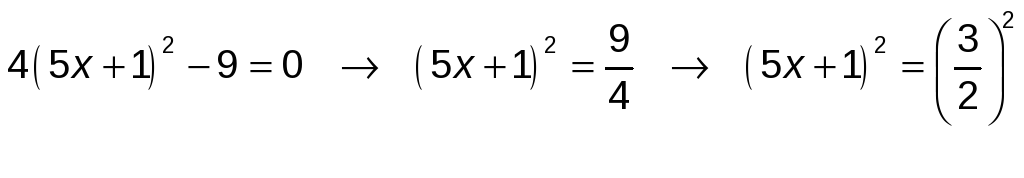
Así:
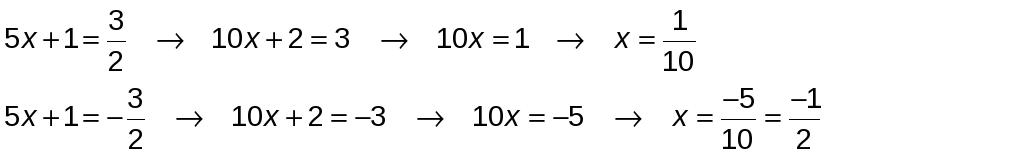
![]()
![]()
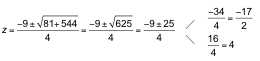
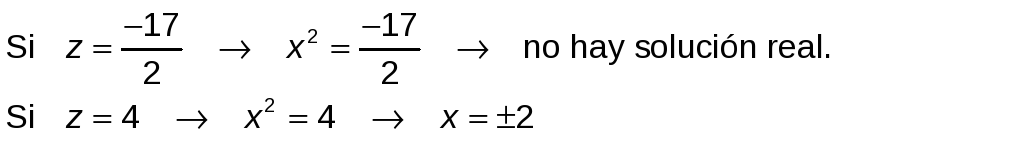
Las soluciones pedidas son x1= 2 y x 2= 2.
Ejercicio nº 2.-
Resuelve las ecuaciones:
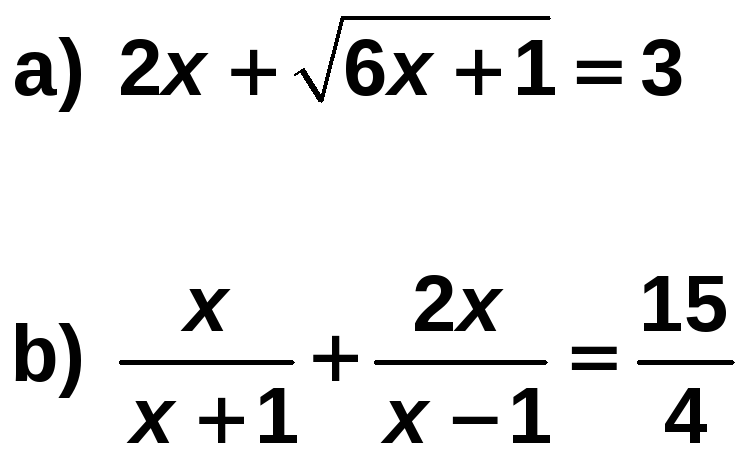
Solución:
![]()
Elevamos ambos miembros al cuadrado:
![]()
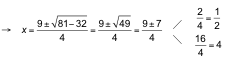
Comprobamos las posibles soluciones sobre la ecuación:
![]()
![]()
![]()
![]()
![]()
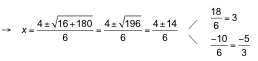
Comprobamos las soluciones:
![]()
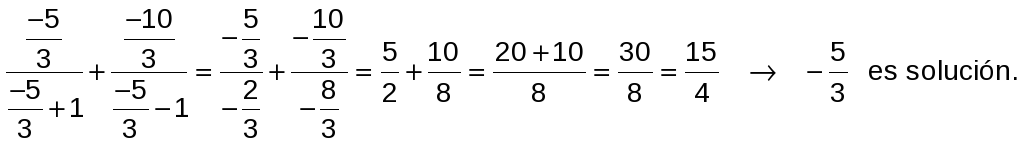
![]()
Ejercicio nº 3.-
![]()
Solución:
Tenemos un producto de factores igualado a 0, luego se ha de cumplir que:
x = 0
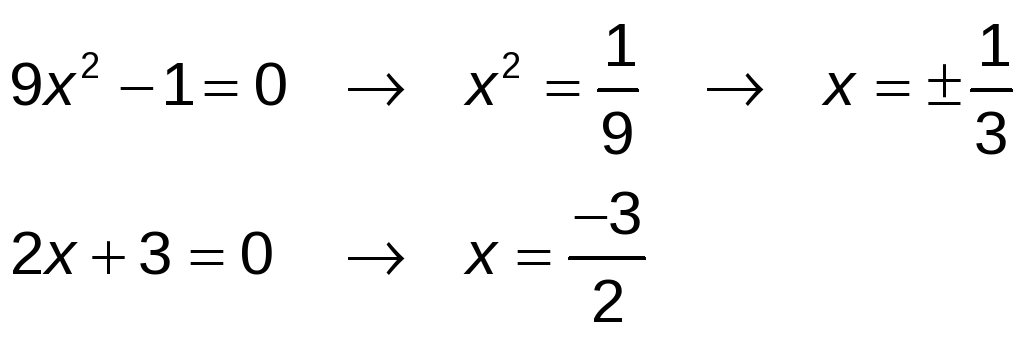
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
a) 3x‒2 + 9x‒1 = 84
b) log2 (x2 + 15) = 6
Solución:
![]()
→ 3x+ 32x= 756
Hacemos cambio de variable 3x= t:
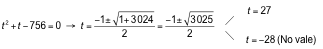
3x= 27 → 3x= 33→ x = 3
b) log2 (x2+ 15) = 6
26= x2+ 15 → 64 = x2+ 15 → 64 ‒ 15 = x2→ 49 = x2
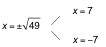
Son válidas las dos soluciones.
Ejercicio nº 5.-
El lado desigual de un triángulo isósceles mide 8 cm y la altura sobre dicho lado mide 1 cm menos que otro de los lados del triángulo. Calcula la longitud de dicho lado.
Solución:
x = "lado del triángulo"
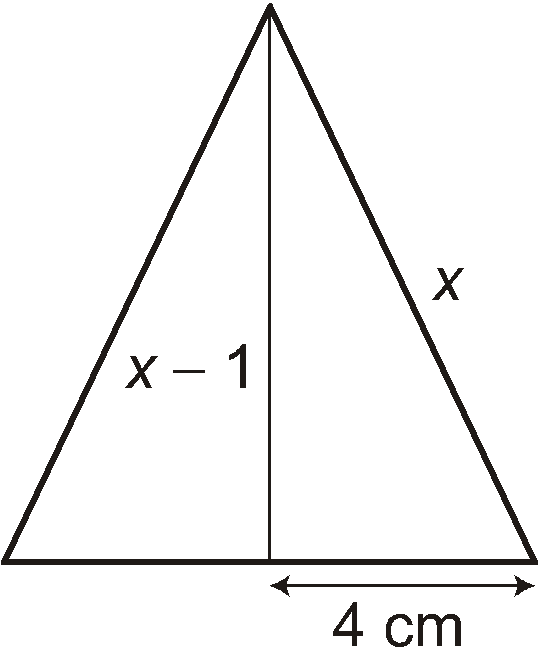
Aplicamos el teorema de Pitágoras al triángulo rectángulo de lados x, x − 1 y 4:
![]()
Luego, x = 8,5 cm es la longitud del lado.
Ejercicio nº 6.-
Halla la solución de este sistema:
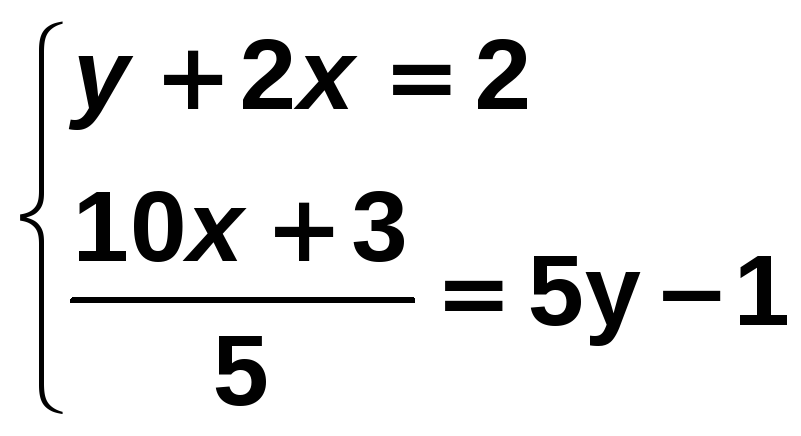
Solución:
Comenzamos por simplificar la segunda ecuación transformándola en otra equivalente:
![]()
El sistema es:
![]()
![]()
![]()
![]()
Luego:
![]()
![]()
Comprobamos la solución:
![]()
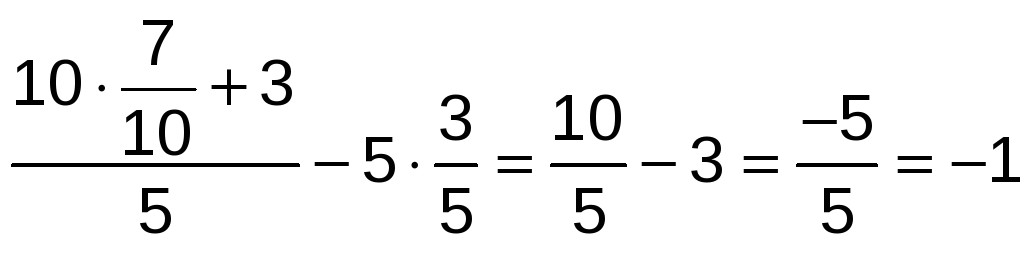
Ejercicio nº 7.-
Resuelve el sistema:
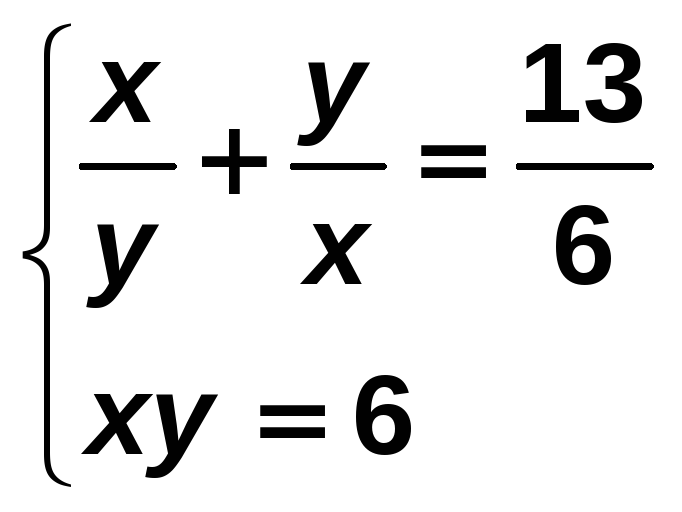
Solución:
Empezamos simplificando la primera ecuación multiplicándola por xy:
![]()
Como xy = 6:
![]()
Por tanto, el sistema a resolver es:
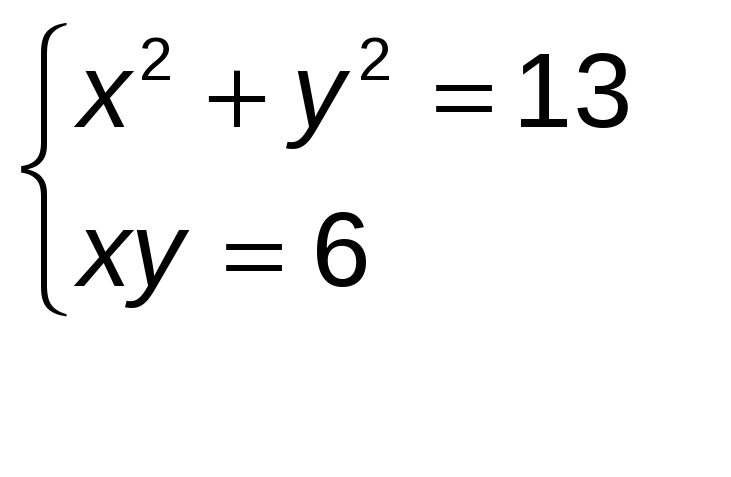
Despejamos y en la segunda ecuación y sustituimos en la primera:
![]()
![]()
Ecuación bicuadrada:
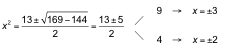
![]()
![]()
Comprobemos si las dos primeras soluciones son, o no, válidas:
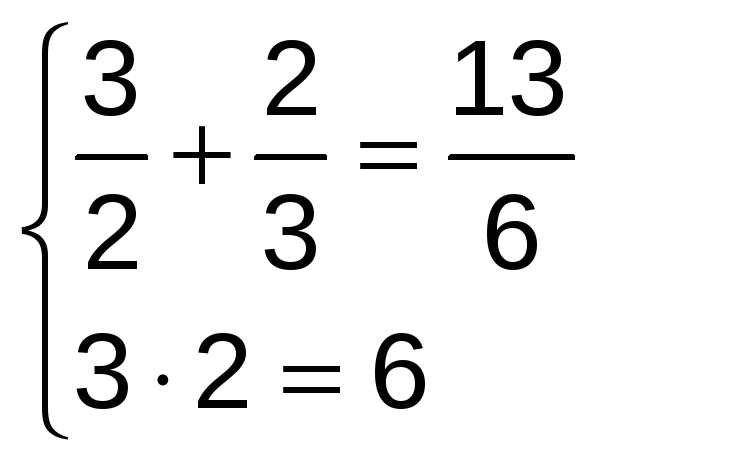
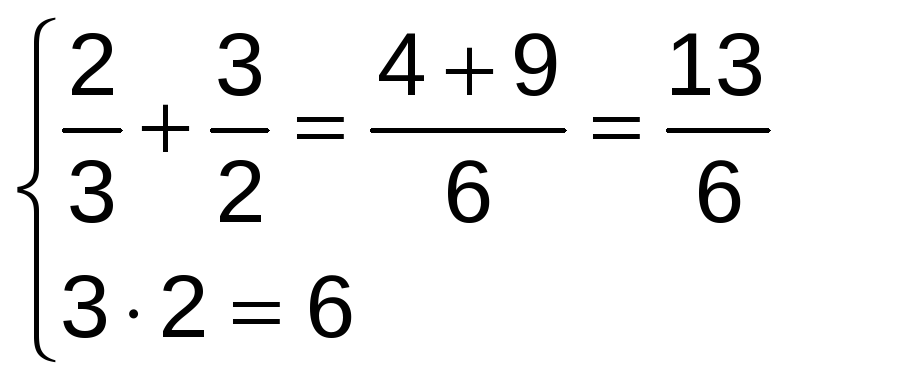
Análogamente se cumpliría para las otras dos. Luego, las soluciones son:
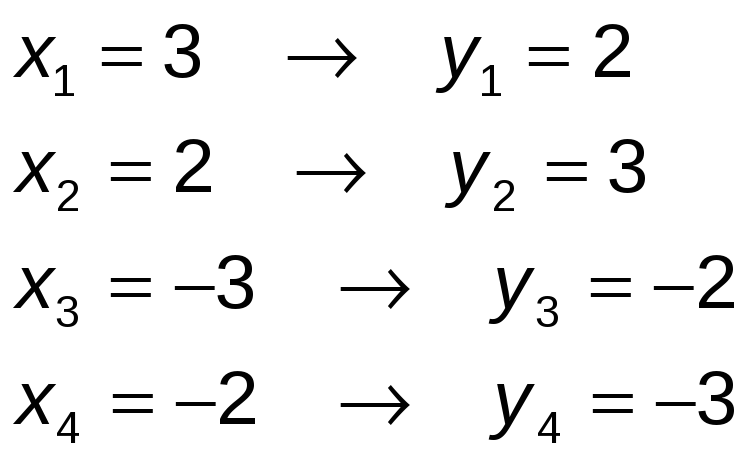
Ejercicio nº 8.-
La diagonal de un rectángulo mide 2 cm más que uno de los lados. Calcula las dimensiones del rectángulo sabiendo que su perímetro es de 14 cm.
Solución:
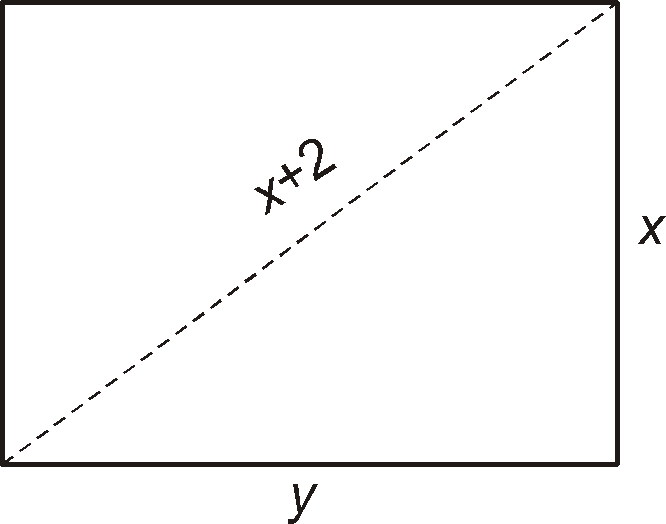
![]()
Despejamos y en la primera ecuación y sustituimos en la segunda:
![]()
![]()
![]()
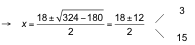
Calculamos el valor de y :
![]()
Luego las dimensiones del rectángulo son 3 cm y 4 cm.
Ejercicio nº 9.-
a) Escribe en forma de intervalo la solución de la siguiente inecuación:
![]()
b) Halla el conjunto de soluciones de la inecuación:
![]()
Solución:
a) Multiplicamos todo por 3 para quitar el denominador:
![]()
![]()
![]()
b) El producto de dos factores es negativo cuando cada uno tiene signos distintos.
En este caso x2≥ 0 siempre, luego para que se cumpla la inecuación, debe verificarse que
![]()
![]()
La solución del sistema es [5, 7).
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
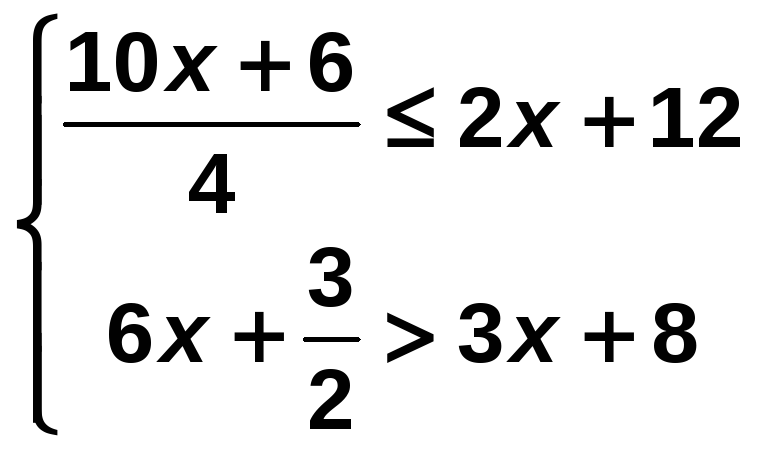
Solución:
Resolvemos cada inecuación por separado; la solución será el conjunto de puntos que cumplan ambas inecuaciones.
![]()
![]()
![]()

Ejercicio nº 11.-
En un triángulo isósceles el lado desigual es la mitad de los lados iguales.
a) Para que el perímetro no supere los 30 cm, ¿qué puedes deducir de la longitud de los lados?
b) ¿Y si además buscamos un perímetro al menos de 15 cm?
Solución:
![]()
![]()
![]()
Los lados iguales no deben superar los 12 cm y el lado desigual ha de ser menor o igual
![]()
![]()
![]()
Luego uniendo ambos apartados llegamos a la siguiente conclusión:
− Los lados iguales, x, miden como mínimo 6 cm y como máximo 12 cm (6 ≤ x ≤ 12).
![]()
Ejercicio nº 12.-
Escribe dos inecuaciones lineales cuya solución común sea el intervalo (−2, 3].
Solución:
Por ejemplo:
![]()
Ejercicio nº 13.-
Dos grifos abiertos a la vez llenan un depósito en 2 horas y media. Abiertos por separado uno de ellos tardaría el doble que el otro en llenar ese mismo depósito. ¿Cuánto tardará cada grifo por separado?
Solución:
Hacemos una tabla para recoger los datos del enunciado y plantear el problema:
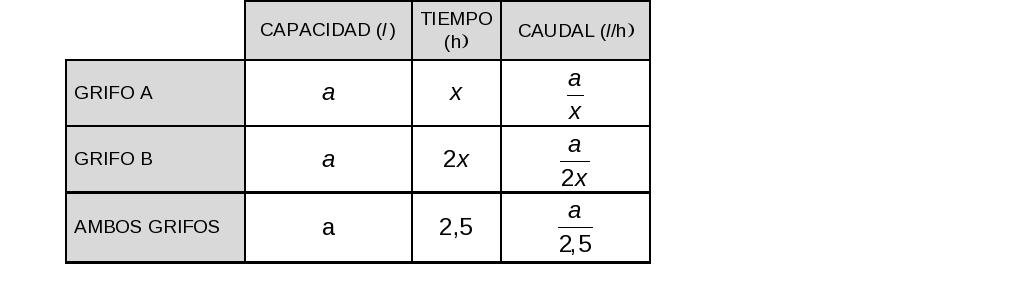
Por tanto:
![]()
Dividiendo entre a:
![]()
El grifo A tardaría en llenar el depósito 3 horas y tres cuartos y el grifo B, 2 · 3,75 = 7,5 horas, es decir, 7 horas y media.







