Indice del artículo
ECUACIONES , INECUACIONES Y SISTEMAS.
Examen2
EXAMEN 3
EXAMEN 4
EXAMEN 5
EXAMEN 6
Todas las páginas

Título de la materia:	Matemáticas orientadas a las Enseñanzas Académicas
Nivel:	ESO 4	Opción:	B
Nombre:		Grupo:
Evaluación:		N.º:
Calificación:		Fecha:

 

Ejercicio nº 1.-

 

Resuelve las siguientes ecuaciones:

 

 

 

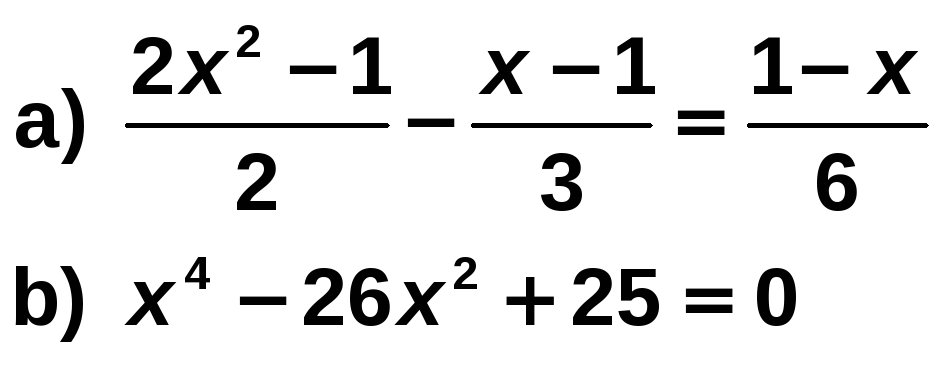
Solución:

 

a) Multiplicamos los dos miembros por 6:

 

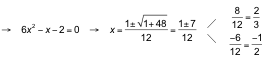
b) Por ser bicuadrada, hacemos el cambio x² = z :

 

 

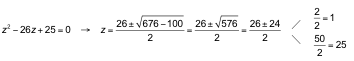
Las soluciones de esta ecuación son x ₁= 1, x ₂= −1 x ₃= 5 y x ₄= −5.

 

 

 

 

Ejercicio nº 2.-

 

Resuelve:

 

 

 

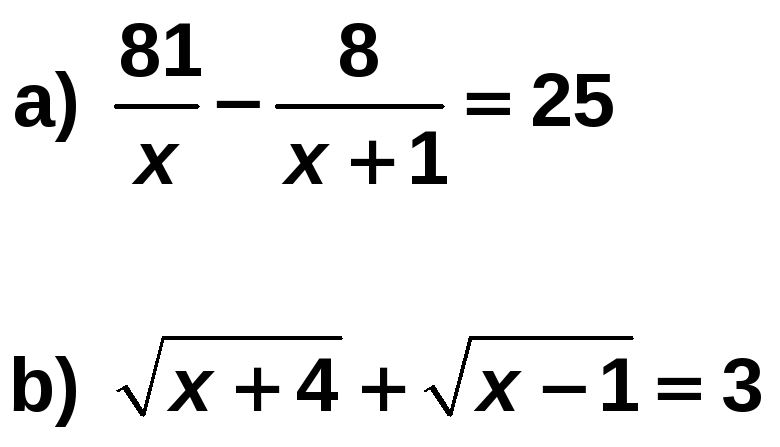
Solución:

 

a) Multiplicamos ambos miembros por x (x + 1):

 

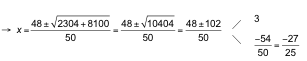
Comprobamos si son, o no, solución en la ecuación inicial:

 

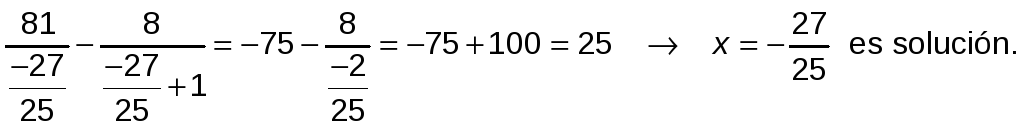
Elevamos ambos miembros al cuadrado:

Volvemos a elevar al cuadrado:

Comprobamos si es, o no, solución:

 

 

 

Ejercicio nº 3.-

 

 

 

Solución:

 

Multiplicando estos tres factores se llega a la ecuación buscada:

 

 

 

 

Ejercicio nº 4.-

 

Resuelve las siguientes ecuaciones:

 

a) 4^x‒1 ‒ 8 · 2^x‒2 + 4 = 0

 

b) log₃ (10x² ‒ 9) = 4

 

 

Solución:

 

Hacemos un cambio de variable: 2^x= t → t² ‒ 8t + 16 = 0

 

Como 2^x= t → 2^x= 2²→ x = 2

 

b) log₃ (10x² ‒ 9) = 4

 

3⁴= 10x² ‒ 9 → 81 = 10x² ‒ 9 → 81 + 9 = 10x²→ 90 = 10x²→

 

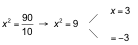
Las dos soluciones son válidas.

 

 

 

 

Ejercicio nº 5.-

 

Un gato, desde su escondite, observa una presa en lo alto de un árbol. Para cazarla corre por el suelo 13 s y trepa por el tronco del árbol durante 15 s, con una velocidad que es la mitad de la que tenía en el suelo. El recorrido total es de 82 m. Averigua a qué distancia se encuentra el pie del árbol del escondite del gato.

 

 

Solución:

 

x = "distancia del escondite al pie del árbol"

 

 

 

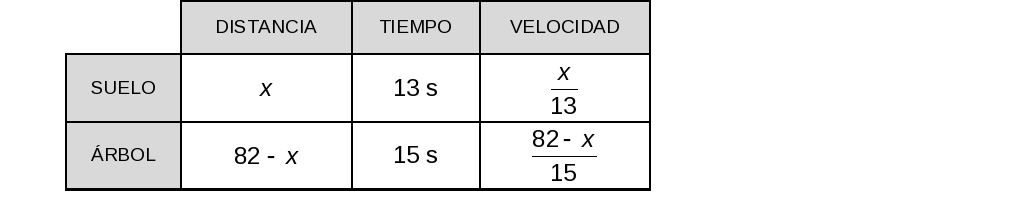
Sabemos que:

Velocidad en el suelo = 2 · Velocidad trepando.

Luego, el planteamiento del problema será:

 

 

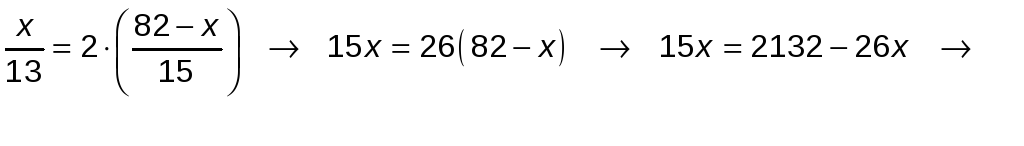
La distancia entre el escondite del gato y el pie del árbol es de 52 m.

 

 

 

 

Ejercicio nº 6.-

 

Resuelve el siguiente sistema:

 

 

 

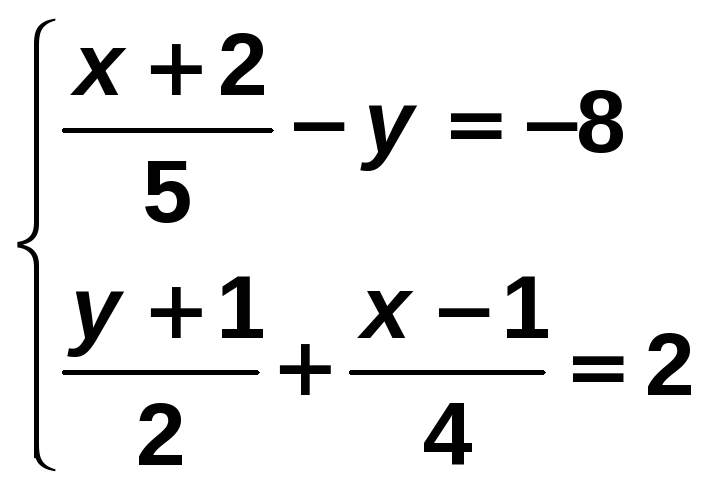
Solución:

 

Comenzamos por simplificar el sistema:

 

 

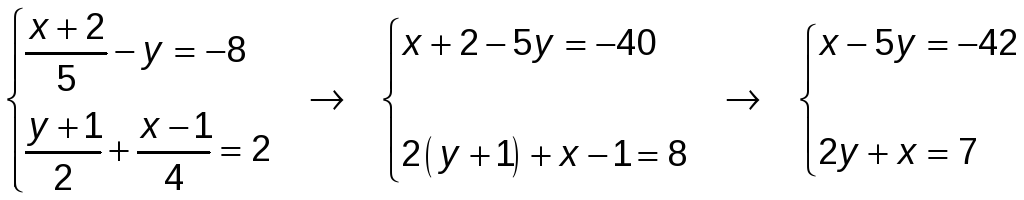
Utilizaremos el método de reducción en x, multiplicando la primera ecuación por −1:

 

 

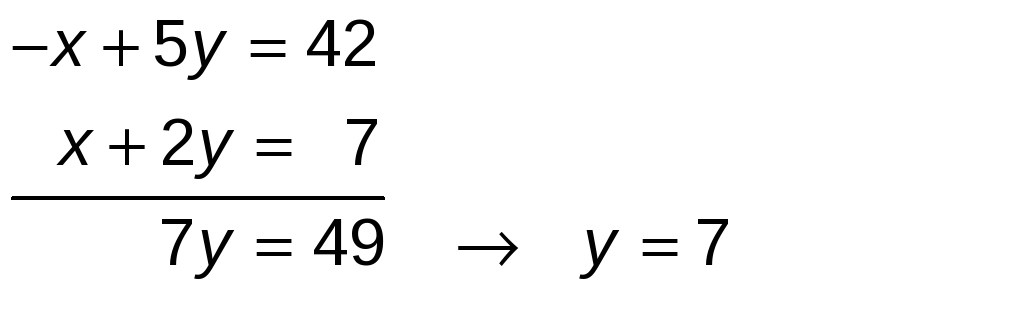
Calculamos el valor de x:

 

x = 7 − 2y → x = 7 − 2 · 7 → x = 7 − 14 → x = −7

 

 

La solución que cumple el sistema es: x = −7, y = 7

 

Comprobamos dicha solución:

 

 

 

 

 

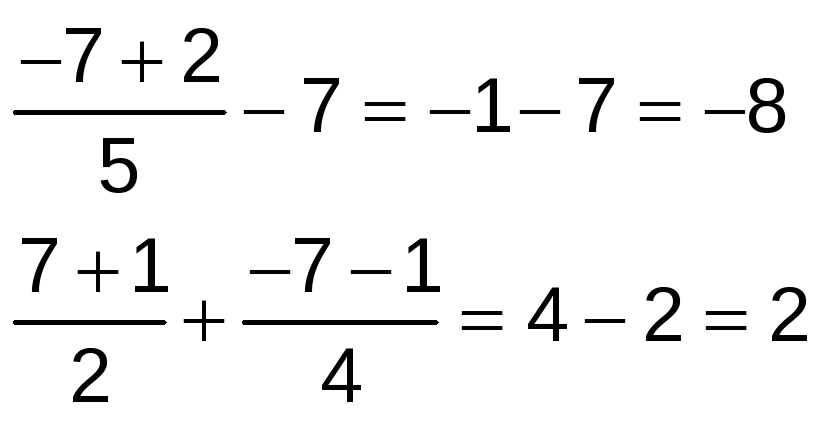
Ejercicio nº 7.-

 

Resuelve el sistema de ecuaciones:

 

 

 

Solución:

 

Despejamos y de la segunda ecuación y sustituimos en la primera:

 

 

 

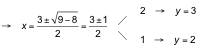
Las soluciones son:

 

 

 

 

 

Ejercicio nº 8.-

 

Un grupo de estudiantes organiza una excursión para lo cual alquilan un autocar cuyo precio es de 540 €. Al salir, no se presentan 6 estudiantes y esto hace que cada uno de los otros pague 3 € más. Calcula el número de estudiantes que fueron a la excursión y que cantidad pagó cada uno.

 

 

Solución:

 

x = "nº de estudiantes que organizan la excursión"

y = "precio que hubiera pagado cada estudiante que organizaba la excursión"

 

El sistema a resolver será:

 

 

 

 

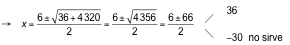
El precio por alumno sería:

 

Luego, van 30 estudiantes a la excursión y cada uno paga 18 €.

 

 

 

 

Ejercicio nº 9.-

 

a) Resuelve la siguiente inecuación y escribe la solución en forma de intervalo:

 

 

b) Resuelve:

(x + 7)(3 ‒ x) ≥ 0

 

 

Solución:

 

a) Multiplicamos por 8 la inecuación y agrupamos los términos como en las ecuaciones:

 

 

La solución buscada es [0, +∞).

 

 

b) Un producto es mayor que 0 cuando ambos factores son del mismo signo.

Estudiamos los signos de x + 7 y de 3 − x:

 

 

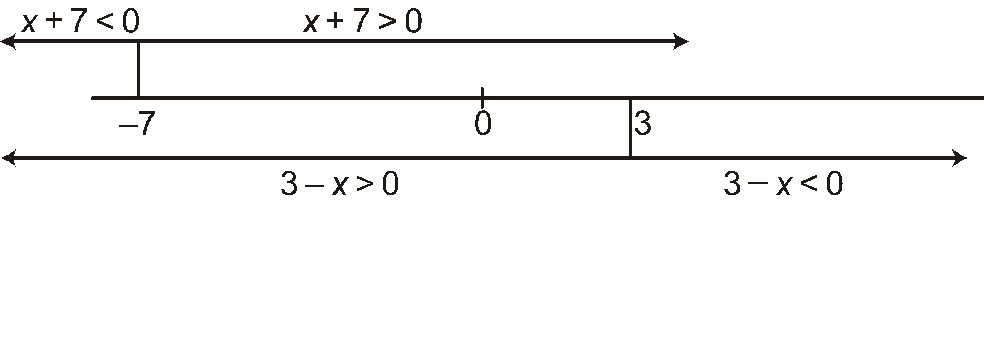
El conjunto de soluciones son los números comprendidos entre −7 y 3, ambos incluidos. Es decir, [−7, 3].

 

 

 

 

Ejercicio nº 10.-

 

Resuelve el siguiente sistema de inecuaciones:

 

 

 

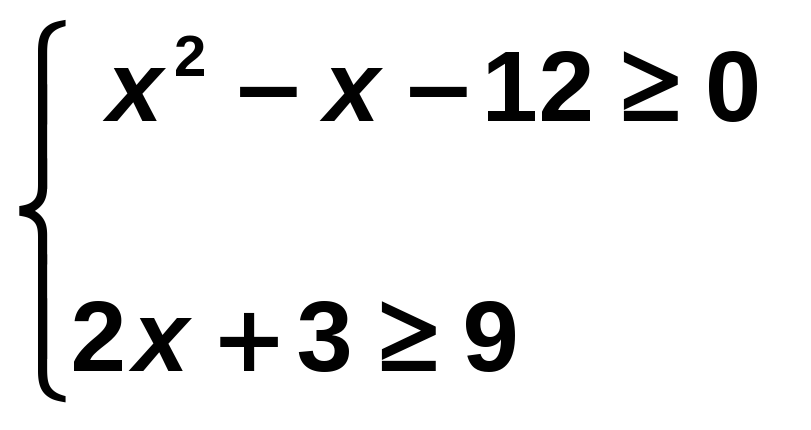
Solución:

 

Resolvemos cada inecuación por separado y buscamos el conjunto de puntos que cumplan ambas a la vez:

 

 

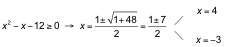
Solución: (‒∞, ‒3] ∪ [4, ∞)

 

2x + 3 ≥ 9 → 2x ≥ 6 → x ≥ 3

 

La solución común a ambas inecuaciones es [4, ∞)

 

 

 

 

 

Ejercicio nº 11.-

 

Si al triple de cierto número le sumas 10 se obtiene al menos su cuadrado. ¿Qué puedes decir de ese número? ¿Y si el número fuera natural?

 

 

Solución:

 

x = “número”

3x + 10 ≥ x² → x²− 3x − 10 ≤ 0

 

Resolvemos la inecuación buscando las soluciones de la ecuación x²− 3x − 10 = 0.

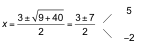
Estudiamos el signo de x²− 3x − 10 en los siguientes intervalos:

(−∞, −2) → (−3)²− 3 · (−3) − 10 > 0

(−2, 5) → 0²− 3 · 0 − 10 < 0

(5, +∞) → 6²− 3 · 6 − 10 > 0

El número buscado está en el intervalo [−2, 5].

Si el número buscado fuese natural la solución sería 0, 1, 2, 3, 4 ó 5.

 

 

 

 

Ejercicio nº 12.-

 

Observa la representación gráfica de la recta y = − 3x + 2 y la parábola y = x² − 2x
y responde sin hacer operaciones para qué valores de x es x² − 2x < −3x + 2.

 

 

 

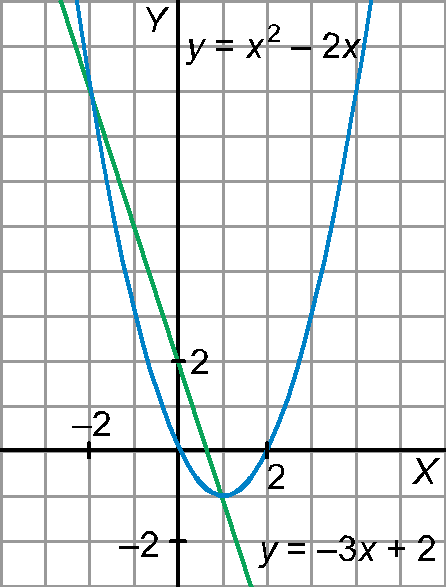
Solución:

 

Observando la gráfica se ve que x²− 2x = −3x + 2 en x = 1 y x = −2.

 

La desigualdad x²− 2x < −3x + 2 se cumple pues entre −2 y 1, es decir, para x perteneciente al intervalo (−2, 1).

 

 

 

 

Ejercicio nº 13.-

 

 

 

Solución:

 

Para que un cociente sea positivo, numerador y denominador han de tener el mismo signo.

Como x²+ 1 > 0 siempre, entonces debe cumplirse que (x + 3) (x − 2) ≥ 0 para asegurarnos un cociente mayor o igual a 0.

(x + 3) (x − 2) = 0 cuando x = −3 o x = 2.

 

 

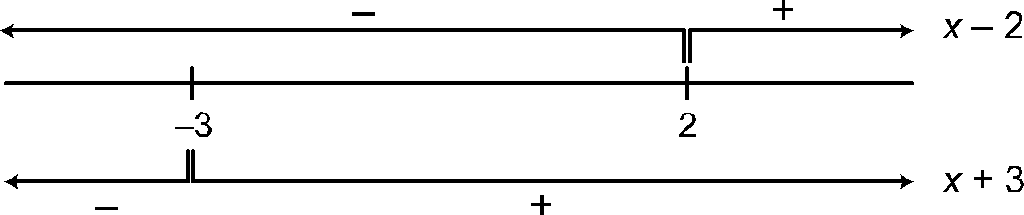
Por tanto, (x + 3) (x − 2) ≥ 0 en aquellas zonas donde ambos signos coinciden, esto es, en (−∞, −3] ∪ [2, +∞), solución también de la inecuación inicial.