Indice del artículo
ECUACIONES , INECUACIONES Y SISTEMAS.
Examen2
EXAMEN 3
EXAMEN 4
EXAMEN 5
EXAMEN 6
Todas las páginas

Título de la materia:	Matemáticas orientadas a las Enseñanzas Académicas
Nivel:	ESO 4	Opción:	E
Nombre:		Grupo:
Evaluación:		N.º:
Calificación:		Fecha:

 

Ejercicio nº 1.-

 

Resuelve:

 

 

 

Solución:

 

a) Efectuamos los paréntesis teniendo en cuenta que todos son productos notables:

 

 

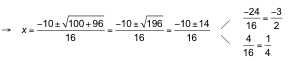
b) Ecuación bicuadrada en la que podemos extraer x ² como factor común:

 

Así:

 

 

 

 

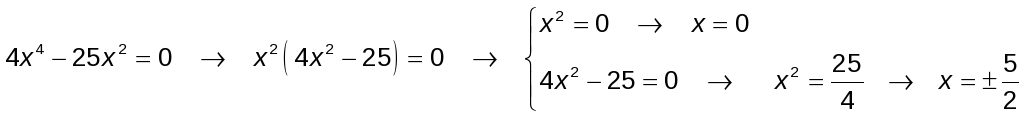
Ejercicio nº 2.-

 

Resuelve las siguientes ecuaciones:

 

 

 

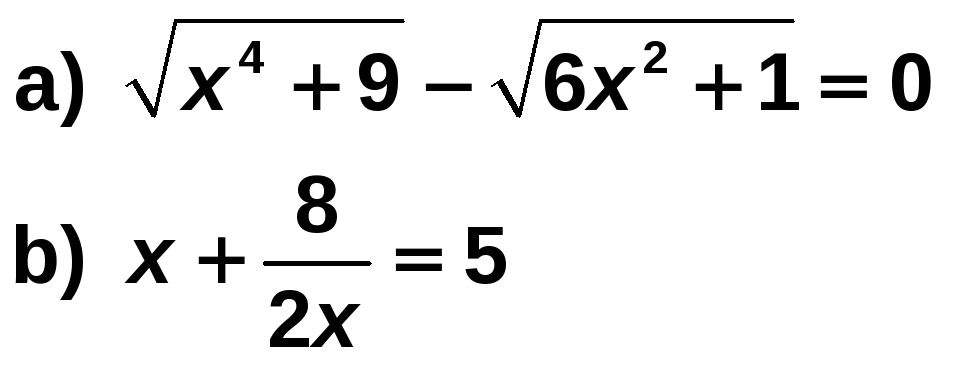
Solución:

 

Elevamos ambos miembros al cuadrado:

Ecuación bicuadrada, que resolvemos haciendo el cambio x ²= z :

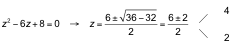
Comprobación:

 

 

b) Multiplicamos ambos miembros por 2x:

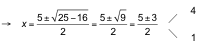
Comprobación de las posibles soluciones:

Las soluciones son x₁= 4 y x₂= 1.

 

 

 

 

Ejercicio nº 3.-

 

 

 

Solución:

 

Para que el producto de varios factores sea 0, alguno de ellos tiene que ser 0. Así:

 

 

 

 

 

 

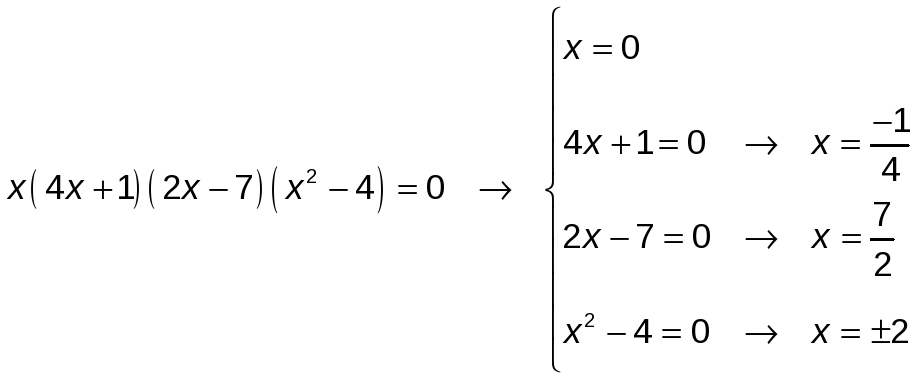
Ejercicio nº 4.-

 

Resuelve las siguientes ecuaciones:

 

a) 3^x + 3^{x + 1} ‒ 3^{x ‒ 1} = 297

 

b) log 3x + log 40 = 2

 

 

Solución:

 

 

Cambio de variable: 3^x= t

 

→ 3^x= 81 → 3^x= 3⁴→ x = 4

 

b) log 3x + log 40 = 2

 

log (3x · 40) = log 100 → 3x · 40 = 100 → 120x = 100 →

 

 

 

 

Ejercicio nº 5.-

 

La base de un rectángulo mide 3 cm más que la altura. Si aumentamos la base en 2 cm y la altura en 3 cm, la superficie del nuevo rectángulo es el doble de la superficie del inicial.

Calcula las dimensiones del rectángulo inicial.

 

 

Solución:

 

 

 

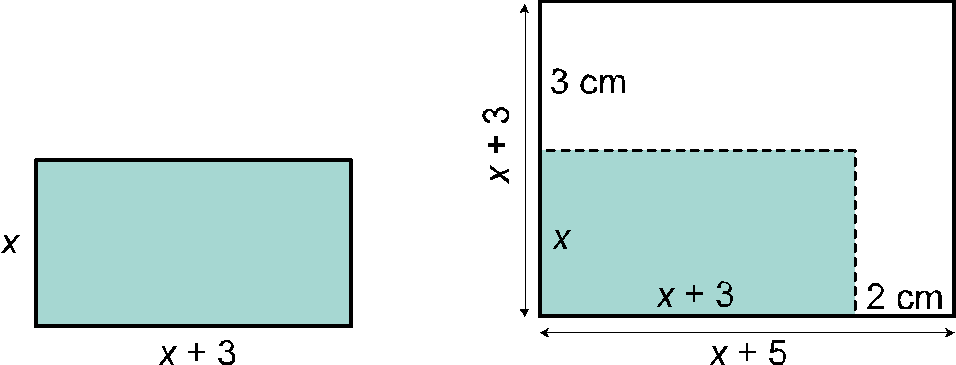
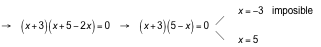
Las dimensiones del rectángulo inicial son 5 cm y 8 cm.

 

 

 

 

Ejercicio nº 6.-

 

Resuelve el siguiente sistema por el método que consideres más adecuado:

 

 

 

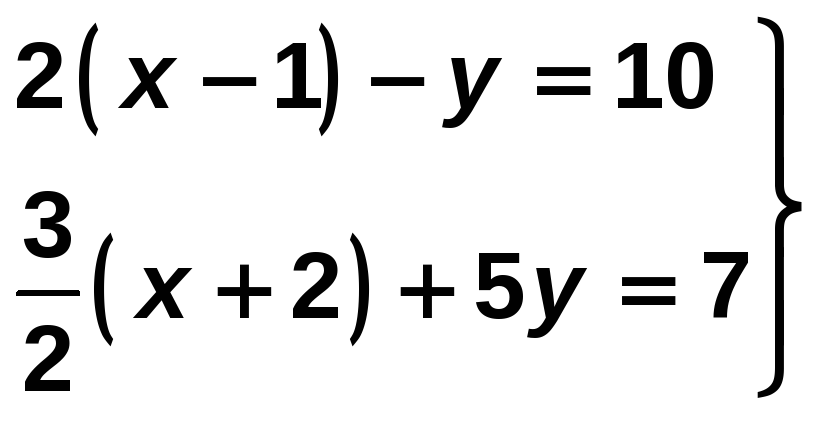
Solución:

 

Comenzamos por simplificar cada una de las ecuaciones del sistema:

 

 

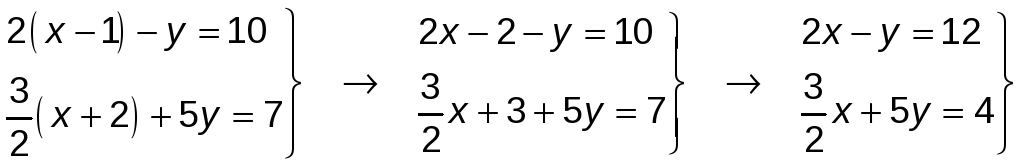
Método de sustitución → Despejamos y de la primera ecuación y sustituimos en la segunda:

 

 

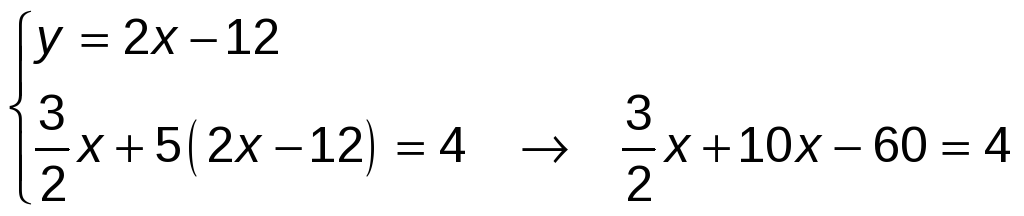
Multiplicamos ambos miembros de la ecuación por 2:

 

Se calcula el valor de y :

 

Comprobamos con la calculadora:

 

2 × [128 a^b/c 23 − 1] − [20 a^b/c 23 ⁺/− ] = 10

 

3a^b/c 2 × [128 a^b/c 23 + 2] + 5 × 20 a^b/c 23 ⁺/− = 7

 

 

 

 

Ejercicio nº 7.-

 

Halla la solución del sistema:

 

 

 

Solución:

 

Multiplicamos la segunda ecuación por −3 para aplicar el método de reducción:

 

 

 

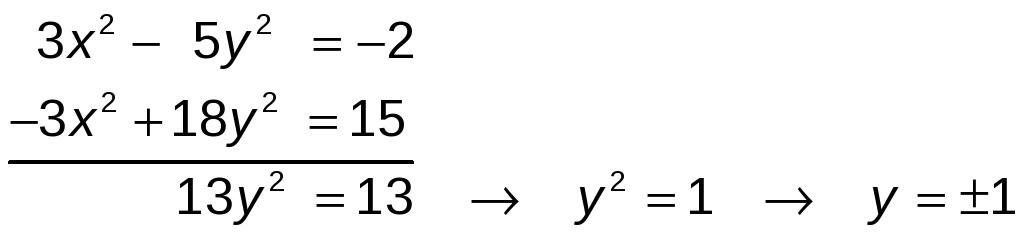
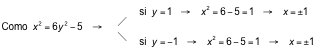
Las soluciones son:

 

 

 

 

 

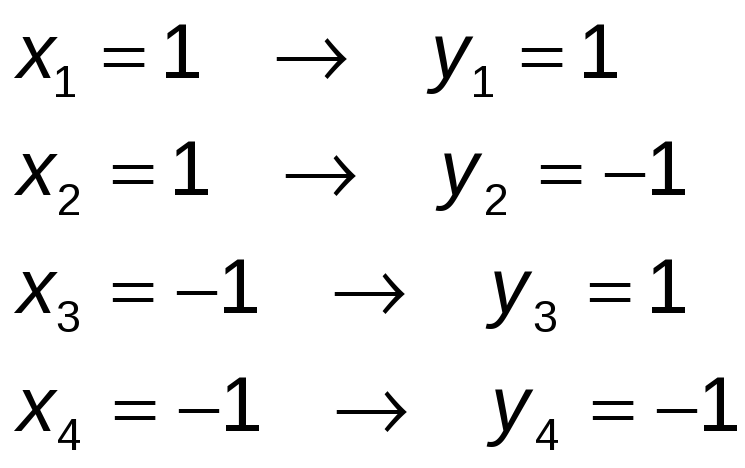
Ejercicio nº 8.-

 

El área de un jardín rectangular mide 900 m² y está rodeado por un paseo de 5 m de ancho, cuya área es de 850 m². Calcula las dimensiones del jardín.

 

 

Solución:

 

Llamamos x, y a las dimensiones del jardín.

 

 

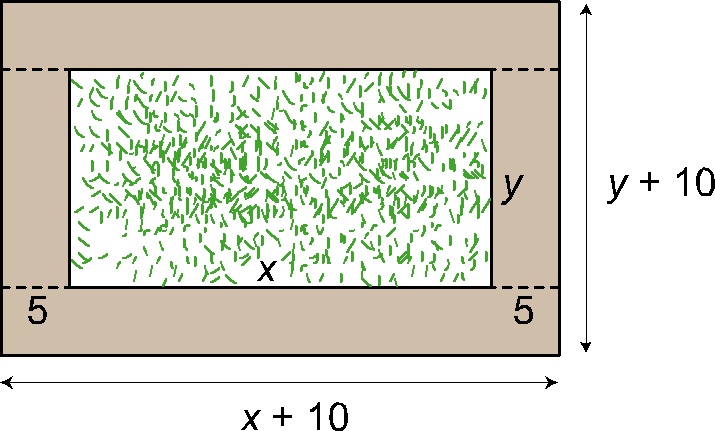
La zona sombreada es el paseo que está formado por dos rectángulos de cada uno de los siguientes tipos:

 

 

 

 

Área del paseo = 850 → 2S₁ + 2S₂ = 850 → S₁ + S₂ = 425 →

→ 5x + 50 + 5y = 425 → 5x + 5y = 375 → x + y = 75

El sistema que resuelve el problema es:

Despejamos x de la 2ª ecuación y sustituimos en la primera:

x = 75 − y

y (75 − y) = 900 → y²− 75y + 900 = 0 →

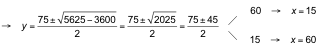
Las dimensiones del jardín son 15 m y 60 m.

 

 

 

 

Ejercicio nº 9.-

 

a) Resuelve gráficamente la inecuación, expresando la solución en forma de intervalo:

 

b) Halla el conjunto de soluciones de la inecuación:

 

x² + 3x ‒ 6 > 8 ‒ 2x

 

 

Solución:

 

 

 

 

 

 

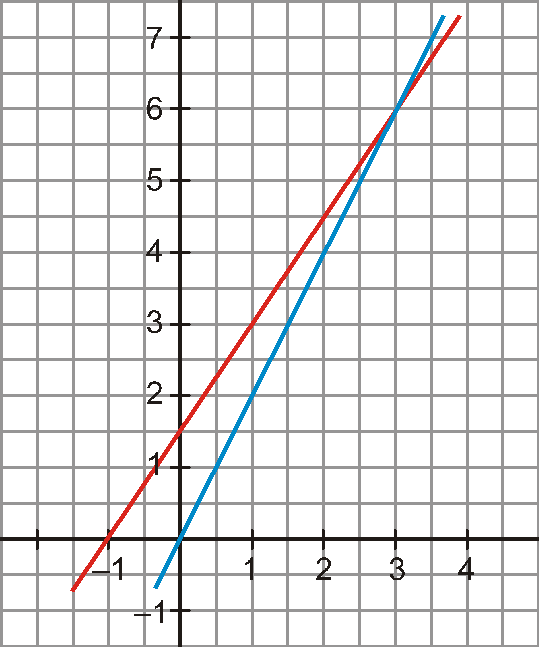
b) x²+ 3x ‒ 6 > 8 ‒ 2x → x²+ 5x ‒ 14 > 0

 

Resolvemos la ecuación x²+ 5x ‒ 14 = 0:

 

 

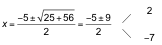
Estudiamos el signo de x²+ 5x − 14 según los valores que damos a x.

 

Los valores −7 y 2 dividen la recta real en tres partes, en cada una de las cuales estudiaremos el signo de x²+ 5x − 14.

 

 

 

 

 

 

 

 

Ejercicio nº 10.-

 

Resuelve el siguiente sistema de inecuaciones:

 

 

 

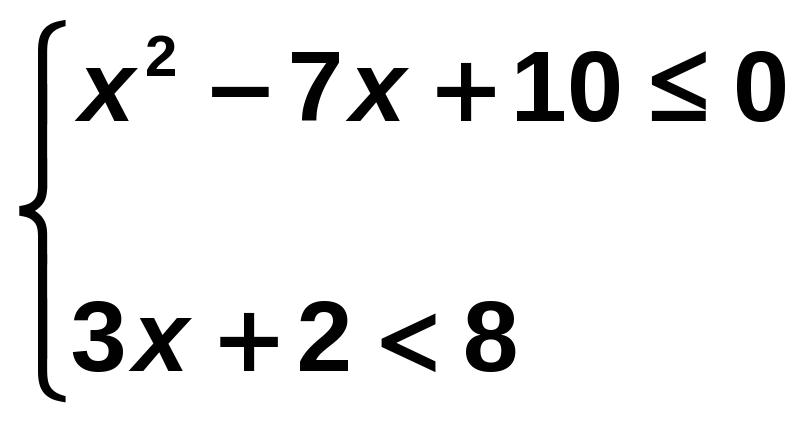
Solución:

 

Resolvemos independientemente cada inecuación y buscamos las soluciones comunes:

 

 

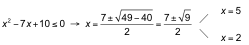
La solución de esta inecuación es [2, 5].

 

3x + 2 < 8 → 3x < 6 → x < 2

 

Este sistema de inecuación no tiene solución.

 

 

 

 

 

Ejercicio nº 11.-

 

El producto de dos números enteros consecutivos es menor que 6. ¿Cuáles pueden ser esos números?

 

 

Solución:

 

Dos números consecutivos son x, x + 1.

 

x(x + 1) < 6 → x²+ x < 6 → x²+ x − 6 < 0

 

Resolvemos la inecuación buscando las raíces de x²+ x − 6.

 

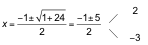
Estudiamos el signo de x²+ x − 6 en cada uno de los siguientes intervalos:

(−∞, −3) → (−4)² − 4 − 6 > 0

(−3, 2) → 0²+ 0 − 6 < 0

(2, +∞) → 3²+ 3 − 6 > 0

 

La solución de la inecuación x²+ x − 6 < 0 es (−3, 2); por tanto los números enteros consecutivos pueden ser −2 y −1, −1 y 0, 0 y 1, 1 y 2.

 

 

 

 

Ejercicio nº 12.-

 

 

 

Solución:

 

 

Buscamos la otra solución de la ecuación 2x²− 9x − 5 = 0.

 

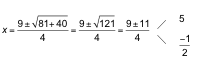
La otra solución es x = 5.

 

 

 

 

Ejercicio nº 13.-

 

Un tractor sube un camino montañoso a 30 km/h y lo baja a 50 km/h. Calcula la velocidad media del recorrido.

 

 

Solución:

 

Hacemos un cuadro para organizar los datos y ayudarnos en el planteamiento del problema.

 

	DISTANCIA (km)	VELOCIDAD	TIEMPO (h)
SUBIDA	d	30 km/h
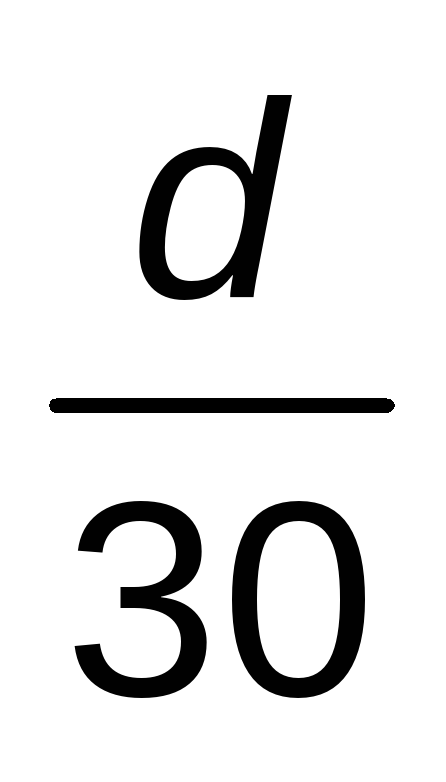
BAJADA	d	50 km/h
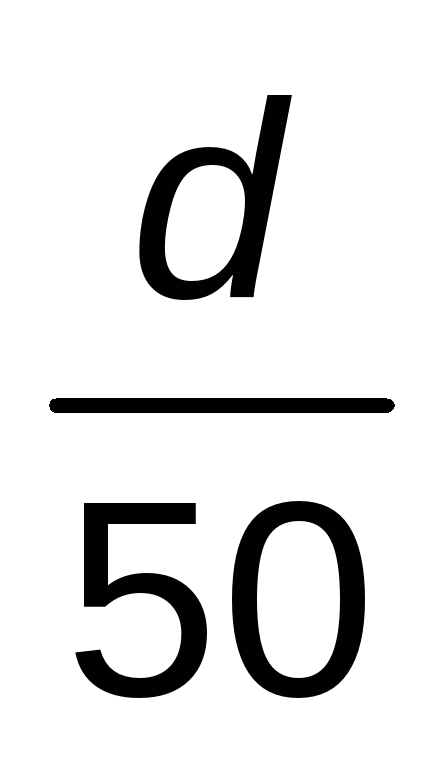
TOTAL RECORRIDO	2d	x

 

 

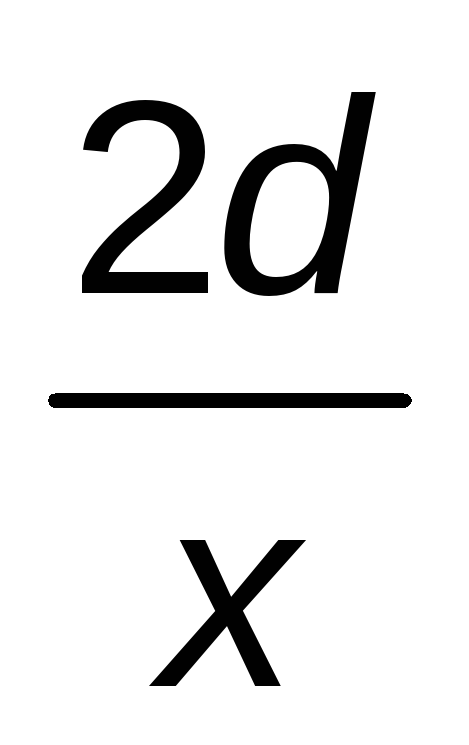
Por tanto:

 

 

Dividiendo entre d:

 

 

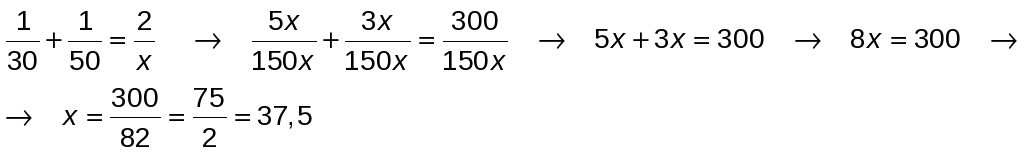
La velocidad media del recorrido ha sido de 37,5 km/h.