| Indice del artículo |
|---|
| ECUACIONES , INECUACIONES Y SISTEMAS. |
| Examen2 |
| EXAMEN 3 |
| EXAMEN 4 |
| EXAMEN 5 |
| EXAMEN 6 |
| Todas las páginas |
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | A |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve las ecuaciones:
![]()
Solución:
a) Sabemos que si a2 = b2, entonces, o bien a = b o bien a = −b.
En este caso:
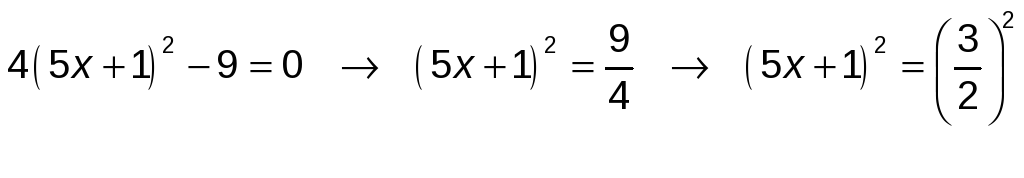
Así:
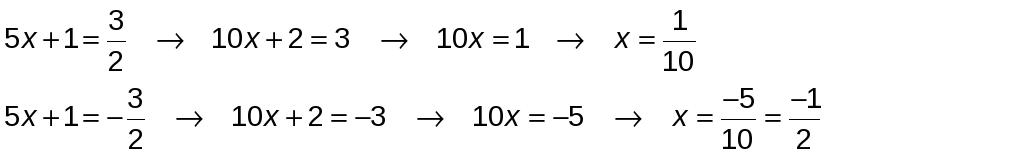
![]()
![]()
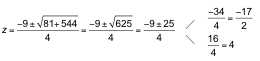
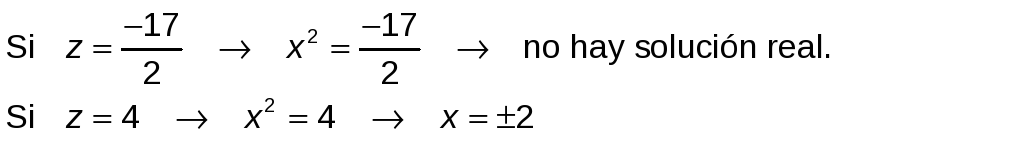
Las soluciones pedidas son x1= 2 y x 2= 2.
Ejercicio nº 2.-
Resuelve las ecuaciones:
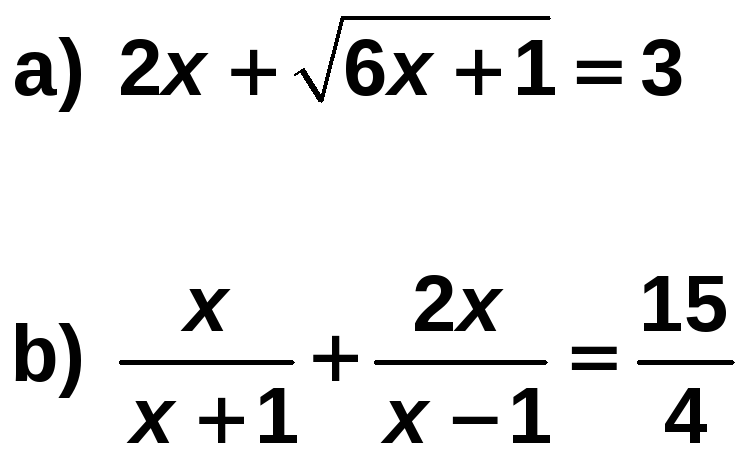
Solución:
![]()
Elevamos ambos miembros al cuadrado:
![]()
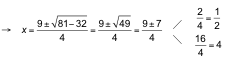
Comprobamos las posibles soluciones sobre la ecuación:
![]()
![]()
![]()
![]()
![]()
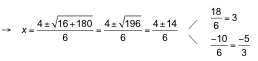
Comprobamos las soluciones:
![]()
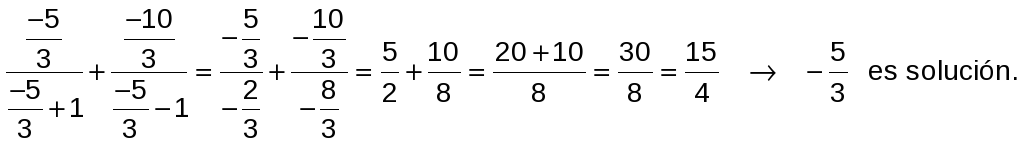
![]()
Ejercicio nº 3.-
![]()
Solución:
Tenemos un producto de factores igualado a 0, luego se ha de cumplir que:
x = 0
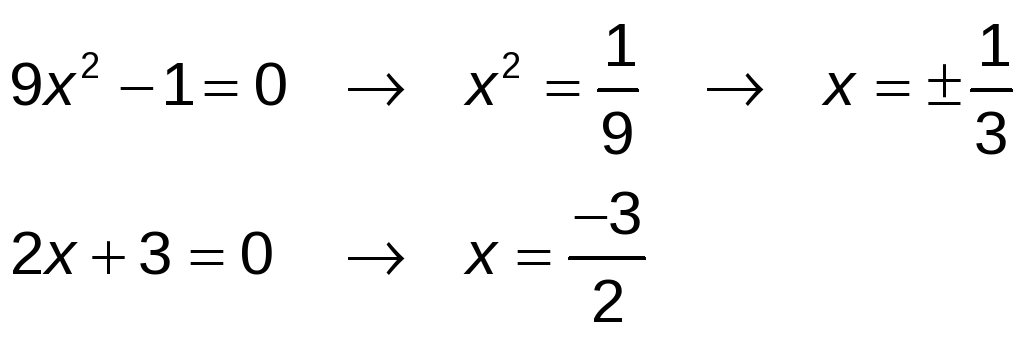
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
a) 3x‒2 + 9x‒1 = 84
b) log2 (x2 + 15) = 6
Solución:
![]()
→ 3x+ 32x= 756
Hacemos cambio de variable 3x= t:
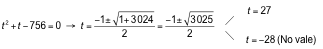
3x= 27 → 3x= 33→ x = 3
b) log2 (x2+ 15) = 6
26= x2+ 15 → 64 = x2+ 15 → 64 ‒ 15 = x2→ 49 = x2
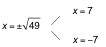
Son válidas las dos soluciones.
Ejercicio nº 5.-
El lado desigual de un triángulo isósceles mide 8 cm y la altura sobre dicho lado mide 1 cm menos que otro de los lados del triángulo. Calcula la longitud de dicho lado.
Solución:
x = "lado del triángulo"
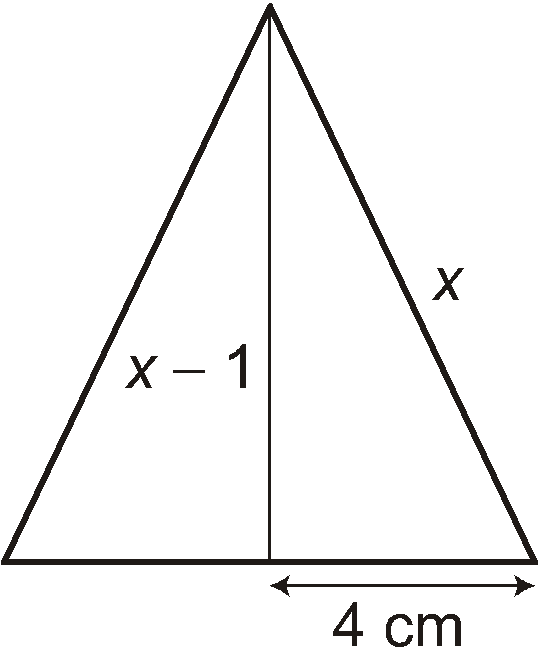
Aplicamos el teorema de Pitágoras al triángulo rectángulo de lados x, x − 1 y 4:
![]()
Luego, x = 8,5 cm es la longitud del lado.
Ejercicio nº 6.-
Halla la solución de este sistema:
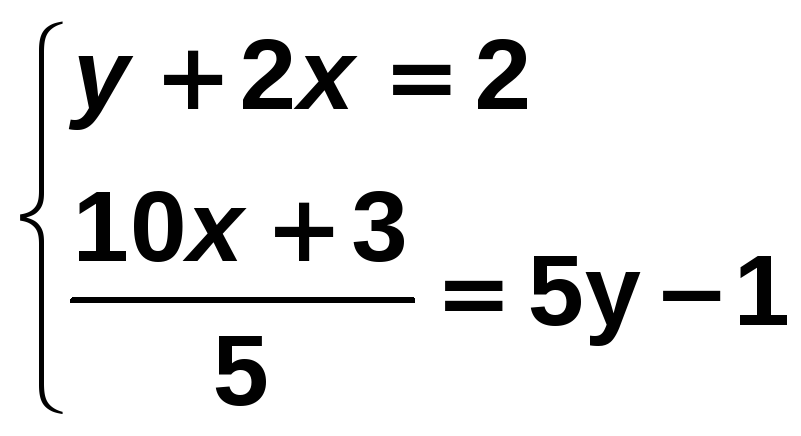
Solución:
Comenzamos por simplificar la segunda ecuación transformándola en otra equivalente:
![]()
El sistema es:
![]()
![]()
![]()
![]()
Luego:
![]()
![]()
Comprobamos la solución:
![]()
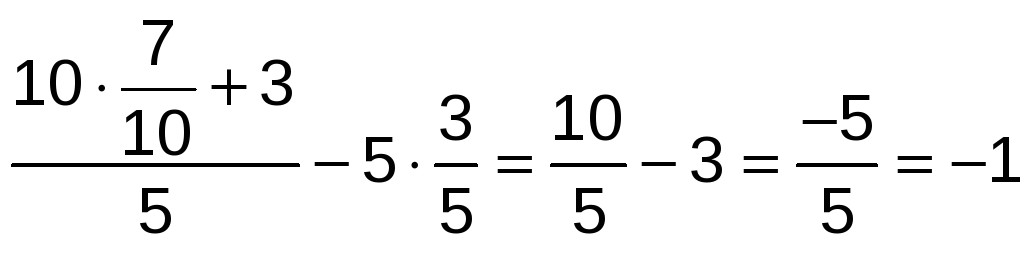
Ejercicio nº 7.-
Resuelve el sistema:
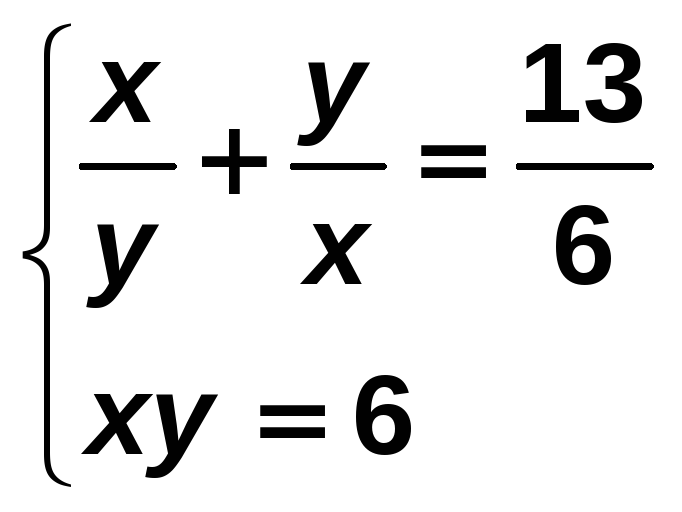
Solución:
Empezamos simplificando la primera ecuación multiplicándola por xy:
![]()
Como xy = 6:
![]()
Por tanto, el sistema a resolver es:
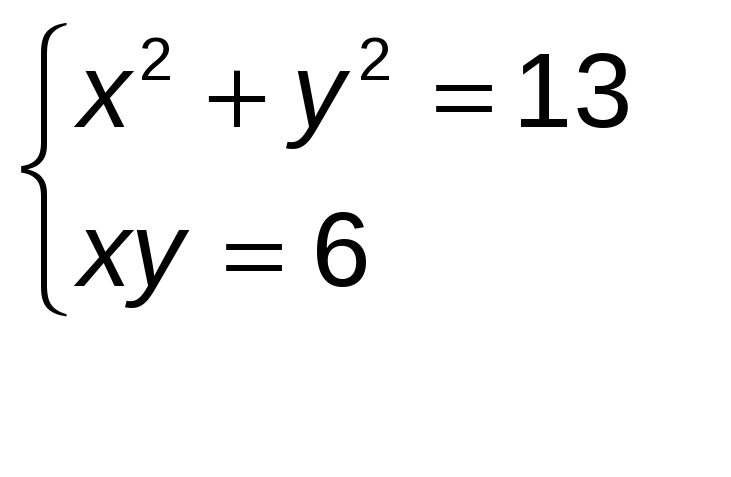
Despejamos y en la segunda ecuación y sustituimos en la primera:
![]()
![]()
Ecuación bicuadrada:
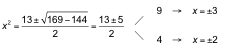
![]()
![]()
Comprobemos si las dos primeras soluciones son, o no, válidas:
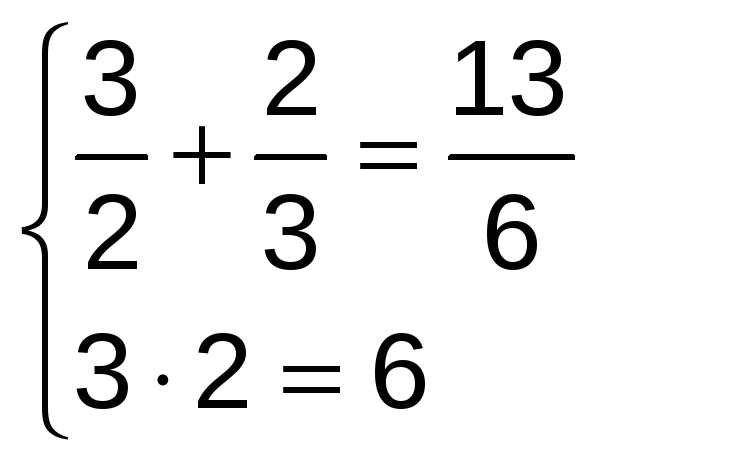
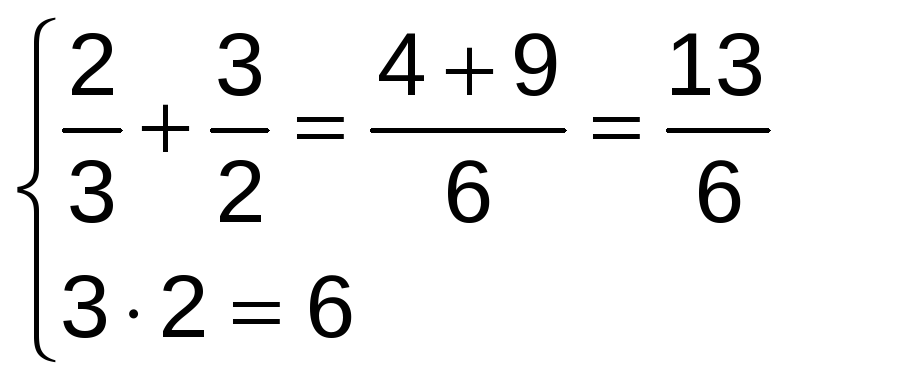
Análogamente se cumpliría para las otras dos. Luego, las soluciones son:
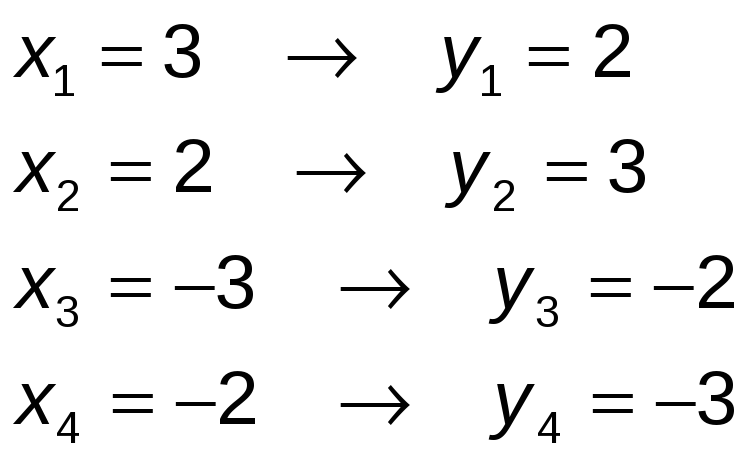
Ejercicio nº 8.-
La diagonal de un rectángulo mide 2 cm más que uno de los lados. Calcula las dimensiones del rectángulo sabiendo que su perímetro es de 14 cm.
Solución:
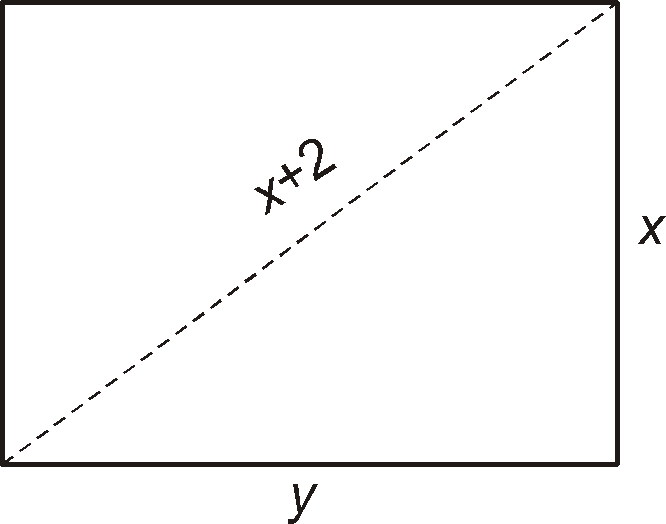
![]()
Despejamos y en la primera ecuación y sustituimos en la segunda:
![]()
![]()
![]()
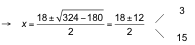
Calculamos el valor de y :
![]()
Luego las dimensiones del rectángulo son 3 cm y 4 cm.
Ejercicio nº 9.-
a) Escribe en forma de intervalo la solución de la siguiente inecuación:
![]()
b) Halla el conjunto de soluciones de la inecuación:
![]()
Solución:
a) Multiplicamos todo por 3 para quitar el denominador:
![]()
![]()
![]()
b) El producto de dos factores es negativo cuando cada uno tiene signos distintos.
En este caso x2≥ 0 siempre, luego para que se cumpla la inecuación, debe verificarse que
![]()
![]()
La solución del sistema es [5, 7).
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
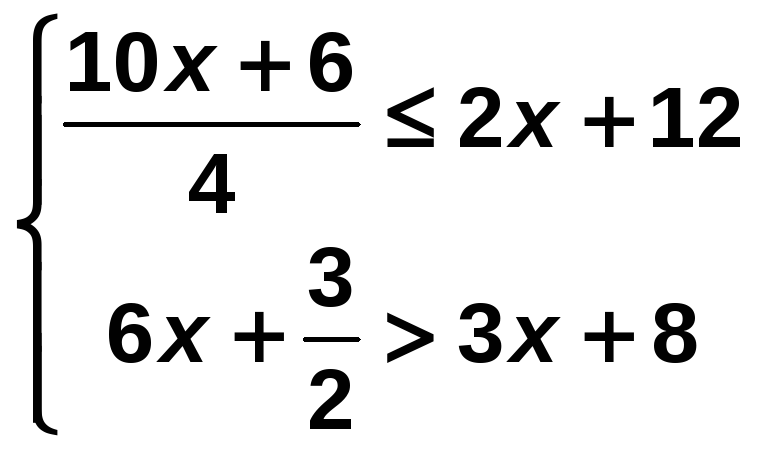
Solución:
Resolvemos cada inecuación por separado; la solución será el conjunto de puntos que cumplan ambas inecuaciones.
![]()
![]()
![]()

Ejercicio nº 11.-
En un triángulo isósceles el lado desigual es la mitad de los lados iguales.
a) Para que el perímetro no supere los 30 cm, ¿qué puedes deducir de la longitud de los lados?
b) ¿Y si además buscamos un perímetro al menos de 15 cm?
Solución:
![]()
![]()
![]()
Los lados iguales no deben superar los 12 cm y el lado desigual ha de ser menor o igual
![]()
![]()
![]()
Luego uniendo ambos apartados llegamos a la siguiente conclusión:
− Los lados iguales, x, miden como mínimo 6 cm y como máximo 12 cm (6 ≤ x ≤ 12).
![]()
Ejercicio nº 12.-
Escribe dos inecuaciones lineales cuya solución común sea el intervalo (−2, 3].
Solución:
Por ejemplo:
![]()
Ejercicio nº 13.-
Dos grifos abiertos a la vez llenan un depósito en 2 horas y media. Abiertos por separado uno de ellos tardaría el doble que el otro en llenar ese mismo depósito. ¿Cuánto tardará cada grifo por separado?
Solución:
Hacemos una tabla para recoger los datos del enunciado y plantear el problema:
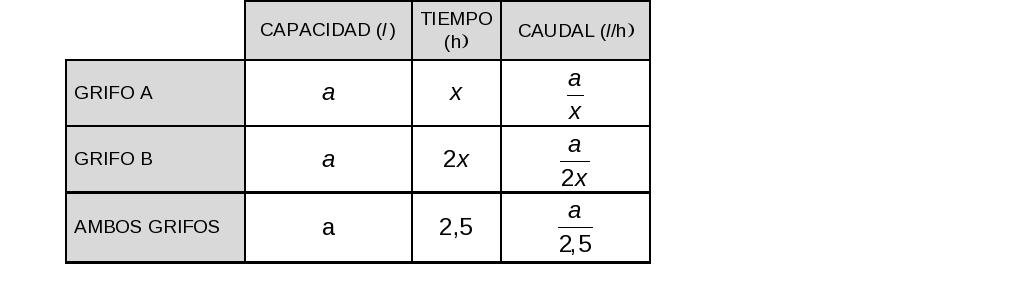
Por tanto:
![]()
Dividiendo entre a:
![]()
El grifo A tardaría en llenar el depósito 3 horas y tres cuartos y el grifo B, 2 · 3,75 = 7,5 horas, es decir, 7 horas y media.
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | B |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve las siguientes ecuaciones:
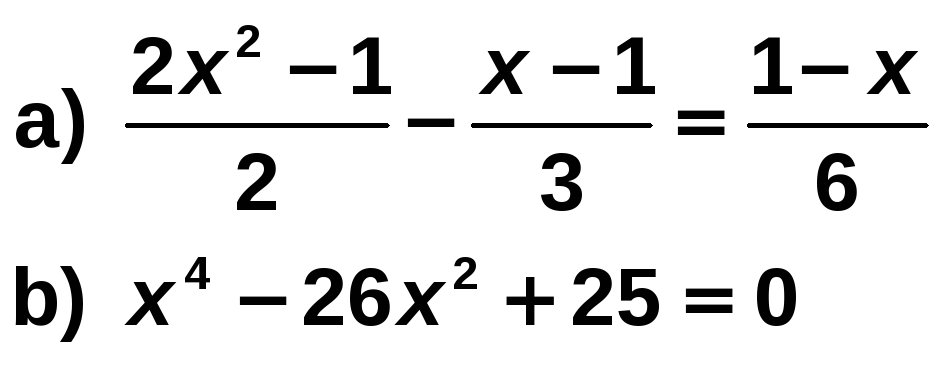
Solución:
a) Multiplicamos los dos miembros por 6:
![]()
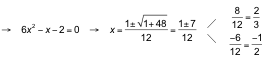
![]()
b) Por ser bicuadrada, hacemos el cambio x2 = z :
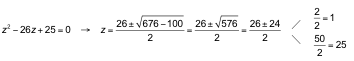
![]()
Las soluciones de esta ecuación son x 1= 1, x 2= −1 x 3= 5 y x 4= −5.
Ejercicio nº 2.-
Resuelve:
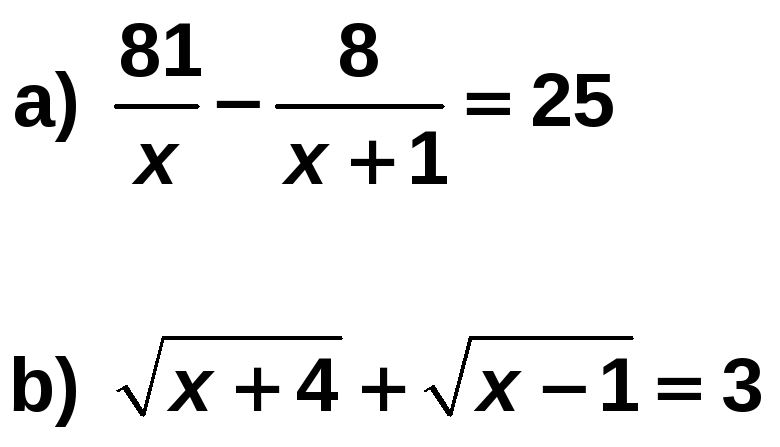
Solución:
a) Multiplicamos ambos miembros por x (x + 1):
![]()
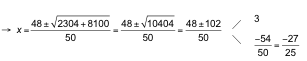
Comprobamos si son, o no, solución en la ecuación inicial:
![]()
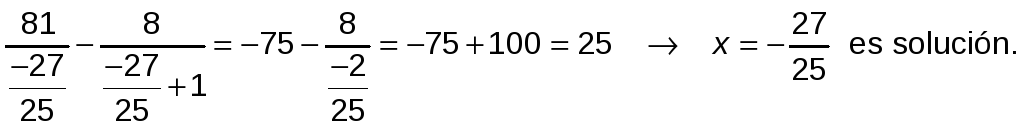
![]()
![]()
Elevamos ambos miembros al cuadrado:
![]()
Volvemos a elevar al cuadrado:
![]()
Comprobamos si es, o no, solución:
![]()
![]()
![]()
Ejercicio nº 3.-
![]()
Solución:
![]()
Multiplicando estos tres factores se llega a la ecuación buscada:
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
a) 4x‒1 ‒ 8 · 2x‒2 + 4 = 0
b) log3 (10x2 ‒ 9) = 4
Solución:
![]()
![]()
Hacemos un cambio de variable: 2x= t → t2 ‒ 8t + 16 = 0
![]()
Como 2x= t → 2x= 22→ x = 2
b) log3 (10x2 ‒ 9) = 4
34= 10x2 ‒ 9 → 81 = 10x2 ‒ 9 → 81 + 9 = 10x2→ 90 = 10x2→
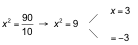
Las dos soluciones son válidas.
Ejercicio nº 5.-
Un gato, desde su escondite, observa una presa en lo alto de un árbol. Para cazarla corre por el suelo 13 s y trepa por el tronco del árbol durante 15 s, con una velocidad que es la mitad de la que tenía en el suelo. El recorrido total es de 82 m. Averigua a qué distancia se encuentra el pie del árbol del escondite del gato.
Solución:
x = "distancia del escondite al pie del árbol"
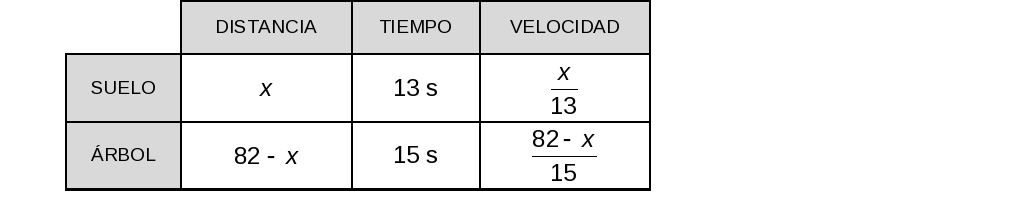
Sabemos que:
Velocidad en el suelo = 2 · Velocidad trepando.
Luego, el planteamiento del problema será:
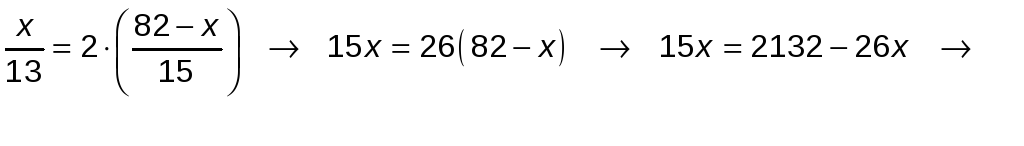
![]()
La distancia entre el escondite del gato y el pie del árbol es de 52 m.
Ejercicio nº 6.-
Resuelve el siguiente sistema:
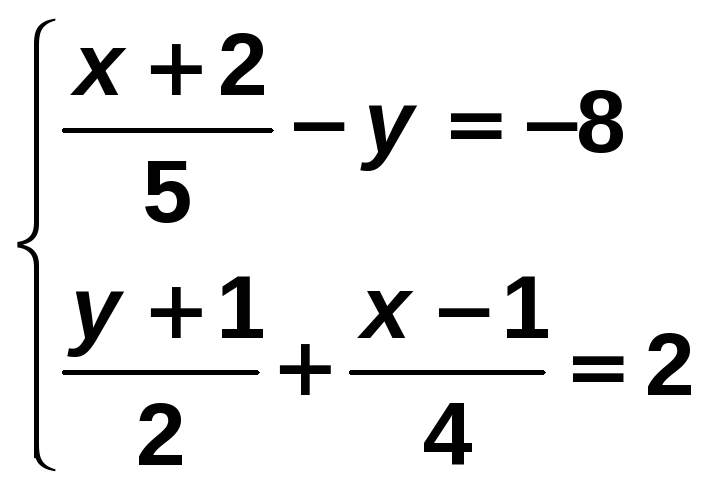
Solución:
Comenzamos por simplificar el sistema:
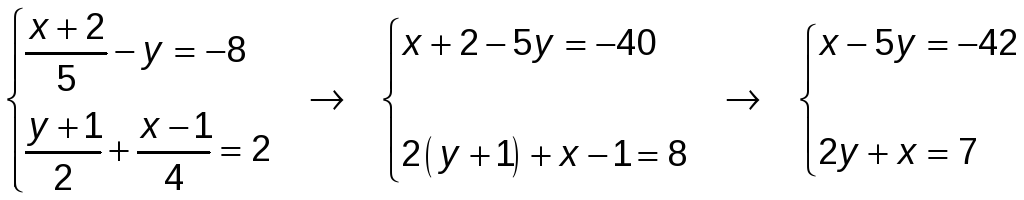
Utilizaremos el método de reducción en x, multiplicando la primera ecuación por −1:
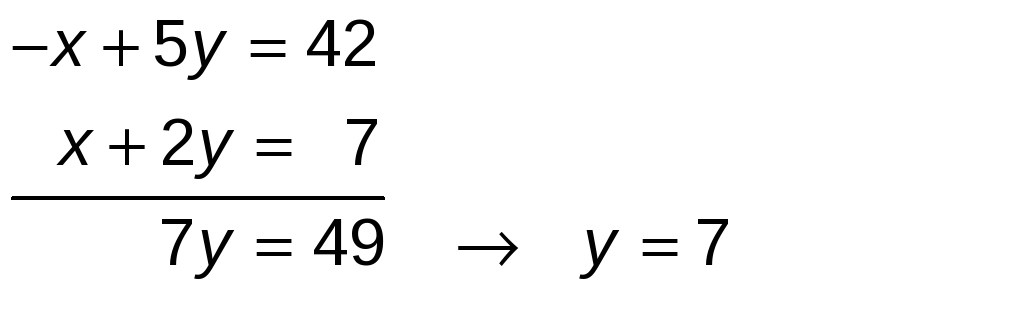
Calculamos el valor de x:
x = 7 − 2y → x = 7 − 2 · 7 → x = 7 − 14 → x = −7
La solución que cumple el sistema es: x = −7, y = 7
Comprobamos dicha solución:
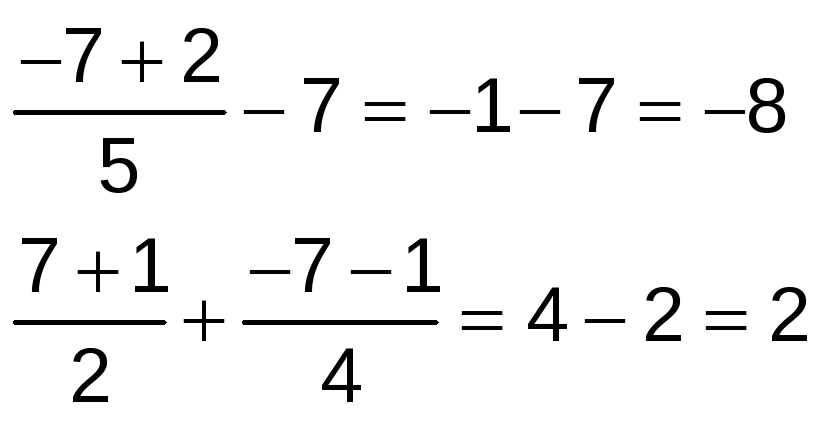
Ejercicio nº 7.-
Resuelve el sistema de ecuaciones:
![]()
Solución:
Despejamos y de la segunda ecuación y sustituimos en la primera:
![]()
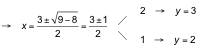
Las soluciones son:
![]()
Ejercicio nº 8.-
Un grupo de estudiantes organiza una excursión para lo cual alquilan un autocar cuyo precio es de 540 €. Al salir, no se presentan 6 estudiantes y esto hace que cada uno de los otros pague 3 € más. Calcula el número de estudiantes que fueron a la excursión y que cantidad pagó cada uno.
Solución:
x = "nº de estudiantes que organizan la excursión"
y = "precio que hubiera pagado cada estudiante que organizaba la excursión"
El sistema a resolver será:

![]()
![]()
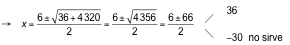
El precio por alumno sería:
![]()
Luego, van 30 estudiantes a la excursión y cada uno paga 18 €.
Ejercicio nº 9.-
a) Resuelve la siguiente inecuación y escribe la solución en forma de intervalo:
![]()
b) Resuelve:
(x + 7)(3 ‒ x) ≥ 0
Solución:
a) Multiplicamos por 8 la inecuación y agrupamos los términos como en las ecuaciones:
![]()
La solución buscada es [0, +∞).
![]()
b) Un producto es mayor que 0 cuando ambos factores son del mismo signo.
Estudiamos los signos de x + 7 y de 3 − x:
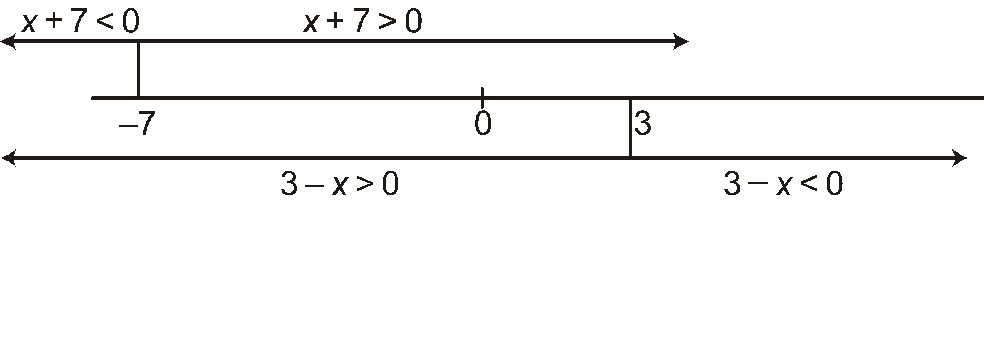
El conjunto de soluciones son los números comprendidos entre −7 y 3, ambos incluidos. Es decir, [−7, 3].
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
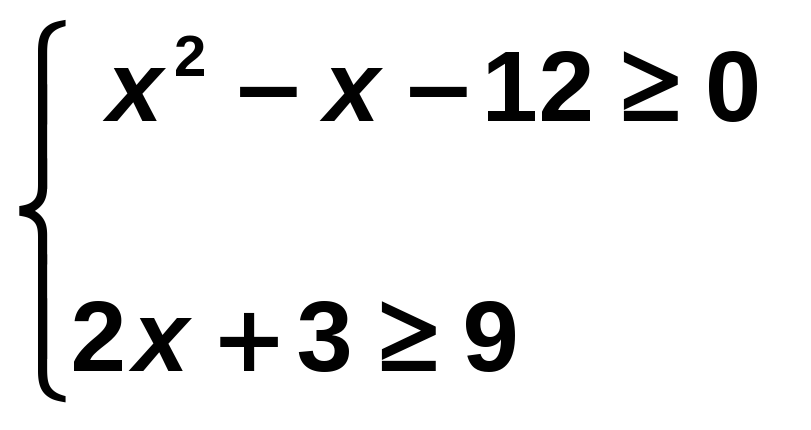
Solución:
Resolvemos cada inecuación por separado y buscamos el conjunto de puntos que cumplan ambas a la vez:
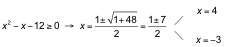

Solución: (‒∞, ‒3] ∪ [4, ∞)
2x + 3 ≥ 9 → 2x ≥ 6 → x ≥ 3
La solución común a ambas inecuaciones es [4, ∞)

Ejercicio nº 11.-
Si al triple de cierto número le sumas 10 se obtiene al menos su cuadrado. ¿Qué puedes decir de ese número? ¿Y si el número fuera natural?
Solución:
x = “número”
3x + 10 ≥ x2 → x2− 3x − 10 ≤ 0
Resolvemos la inecuación buscando las soluciones de la ecuación x2− 3x − 10 = 0.
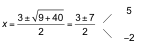
Estudiamos el signo de x2− 3x − 10 en los siguientes intervalos:
(−∞, −2) → (−3)2− 3 · (−3) − 10 > 0
(−2, 5) → 02− 3 · 0 − 10 < 0
(5, +∞) → 62− 3 · 6 − 10 > 0
El número buscado está en el intervalo [−2, 5].
Si el número buscado fuese natural la solución sería 0, 1, 2, 3, 4 ó 5.
Ejercicio nº 12.-
Observa la representación gráfica de la recta y = − 3x + 2 y la parábola y = x2 − 2x
y responde sin hacer operaciones para qué valores de x es x2 − 2x < −3x + 2.
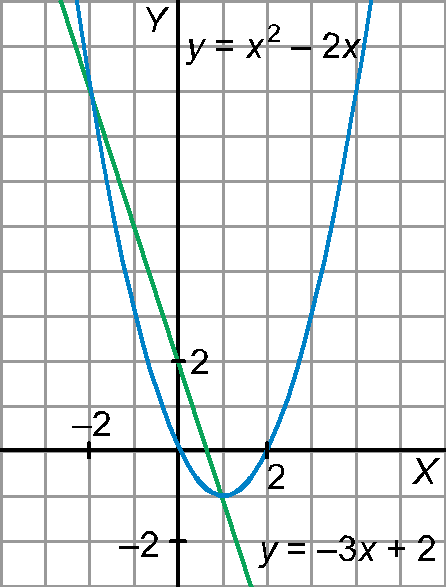
Solución:
Observando la gráfica se ve que x2− 2x = −3x + 2 en x = 1 y x = −2.
La desigualdad x2− 2x < −3x + 2 se cumple pues entre −2 y 1, es decir, para x perteneciente al intervalo (−2, 1).
Ejercicio nº 13.-
![]()
Solución:
Para que un cociente sea positivo, numerador y denominador han de tener el mismo signo.
Como x2+ 1 > 0 siempre, entonces debe cumplirse que (x + 3) (x − 2) ≥ 0 para asegurarnos un cociente mayor o igual a 0.
(x + 3) (x − 2) = 0 cuando x = −3 o x = 2.
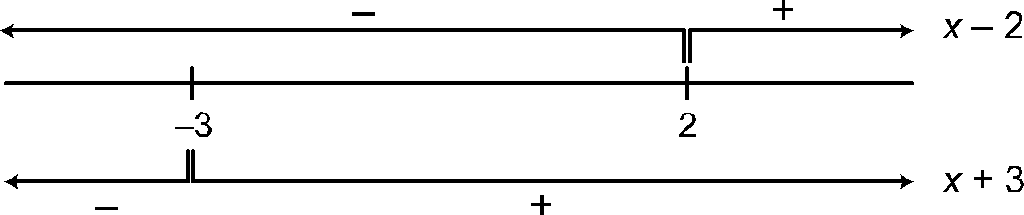
Por tanto, (x + 3) (x − 2) ≥ 0 en aquellas zonas donde ambos signos coinciden, esto es, en (−∞, −3] ∪ [2, +∞), solución también de la inecuación inicial.
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | C |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve las siguientes ecuaciones:
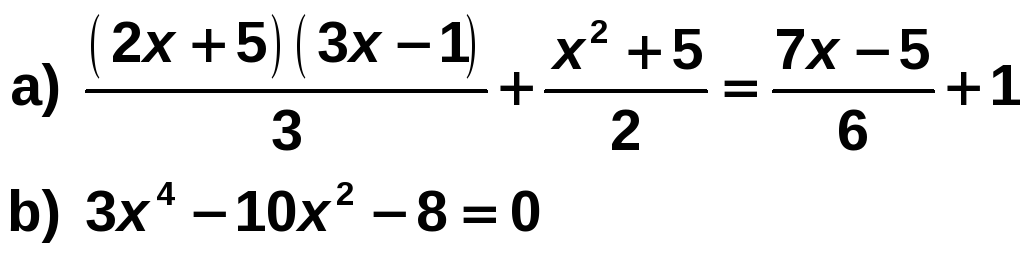
Solución:
a) Multiplicamos ambos miembros por 6:
![]()
![]()
![]()
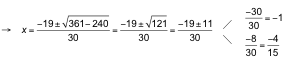
![]()
b) haciendo x2= z, se obtiene:
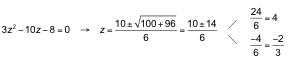
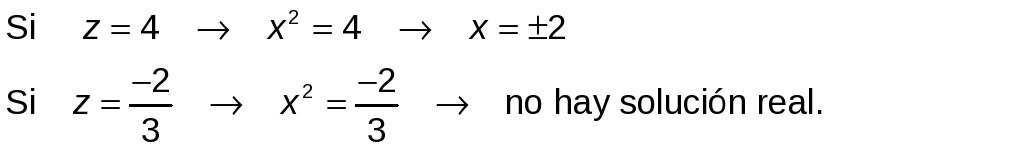
Las soluciones son x1= 2 y x2= −2.
Ejercicio nº 2.-
Resuelve:
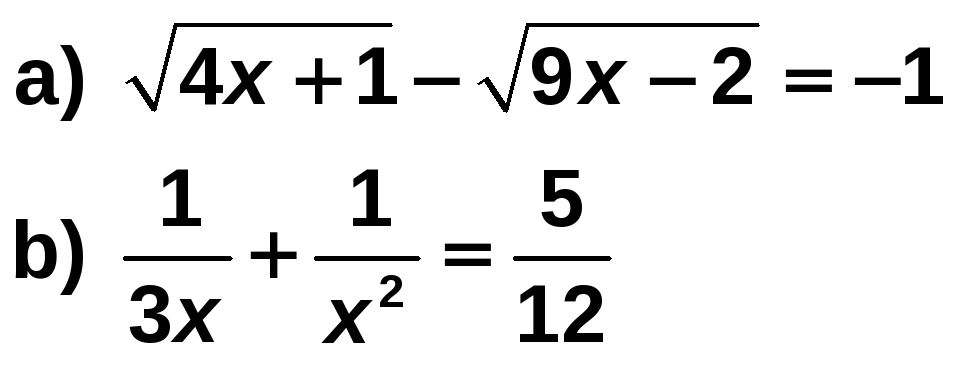
Solución:
![]()
Elevamos al cuadrado ambos miembros de la ecuación:
![]()
Volvemos a elevar al cuadrado:
![]()
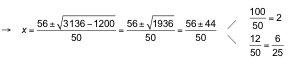
Comprobamos las dos posibles soluciones, sustituyendo en la ecuación inicial:
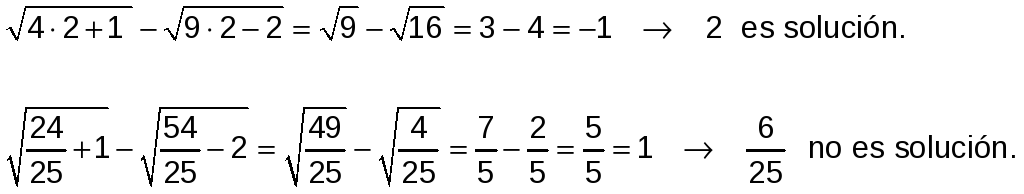
La única solución es x = 2.
b) Multiplicamos ambos miembros por 12x2, que es el mín.c.m. de los denominadores:
![]()
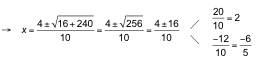
Comprobación:
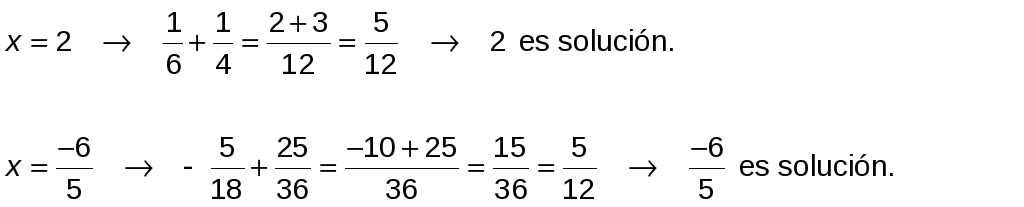
![]()
Ejercicio nº 3.-
![]()
Solución:
Consideramos cuatro polinomios de grado 1 cuyas ecuaciones tengan como raíces los valores
![]()
Se tiene, así:
![]()
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
![]()
b) log2 (6x2 ‒ 2x) = 2
Solución:
![]()
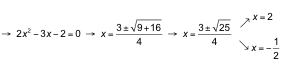
b) log2 (6x2 ‒ 2x) = 2 → 22= 6x2 ‒ 2x → 4 = 6x2 ‒ 2x →
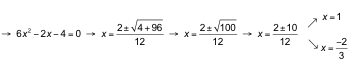
Las dos soluciones son válidas.
Ejercicio nº 5.-
![]()
en reformar la casa, el 10% de la cantidad inicial en ropa y el resto, 260 €, los ahorró. ¿Cuánto dinero heredó?
Solución:
x = "dinero heredado"

La ecuación que resuelve el problema será:
![]()
Multiplicamos ambos miembros por 30:
![]()
![]()
Ejercicio nº 6.-
Resuelve por el método que consideres más apropiado y comprueba la solución obtenida en el siguiente sistema:
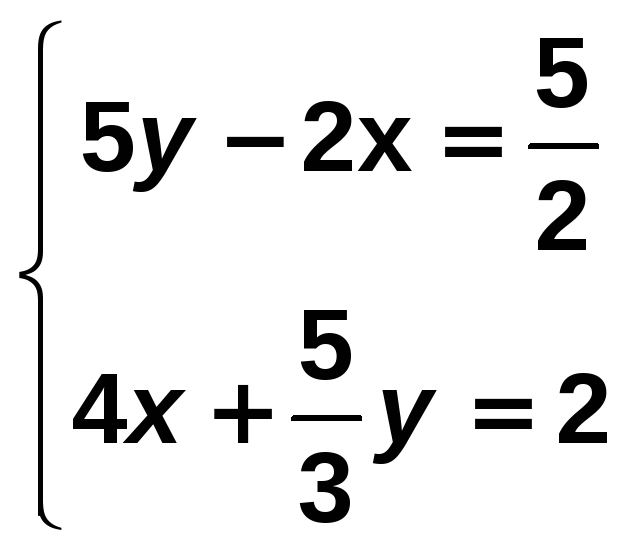
Solución:
Utilizamos el método de reducción en y ; para ello multiplicamos la 2ª ecuación por −3:
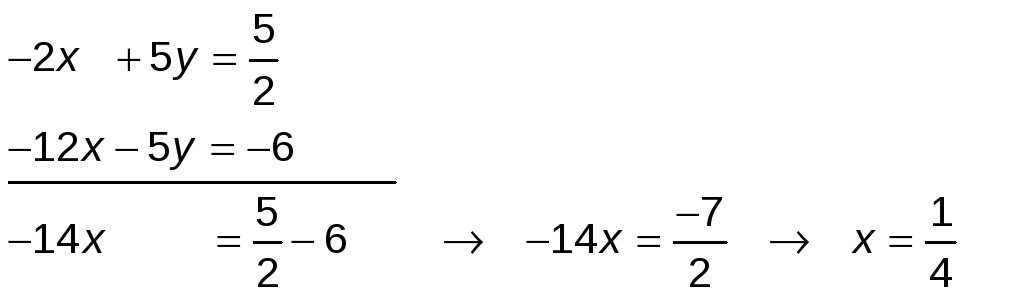
Calculamos y sustituimos el valor de x en la 1ª ecuación:
![]()
![]()
Comprobamos la solución:
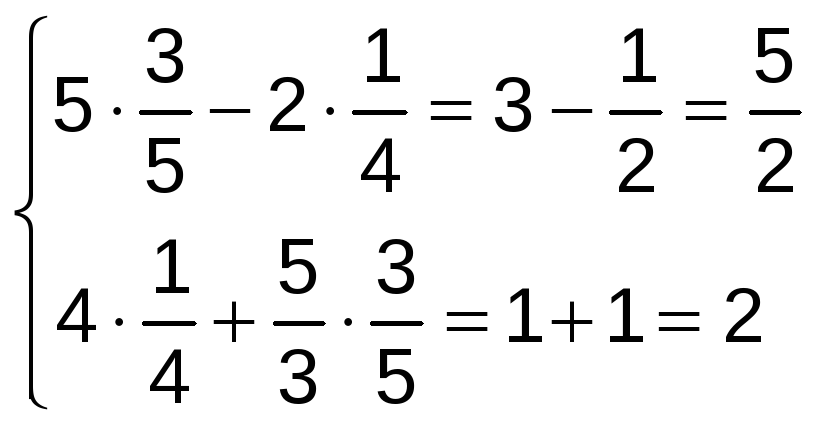
Ejercicio nº 7.-
Resuelve:
![]()
Solución:
![]()
Aplicamos el método de igualación:
![]()
Elevamos al cuadrado los dos miembros de la última igualdad:
![]()
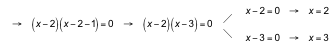
![]()
Comprobamos las soluciones sobre el sistema:
![]()
![]()
Ejercicio nº 8.-
Un bodeguero quiere mezclar vino de calidad superior cuyo precio es de 6 €/l con otro más corriente de 2 €/l. Dispone en total de 315 l. Calcula el número de litros de cada clase para que la mezcla cueste 4,4 €/l.
Solución:
x = “litros del vino que cuesta 6 €/ l ”
y = “litros del vino que cuesta 2 €/ l ”
El sistema a resolver será:
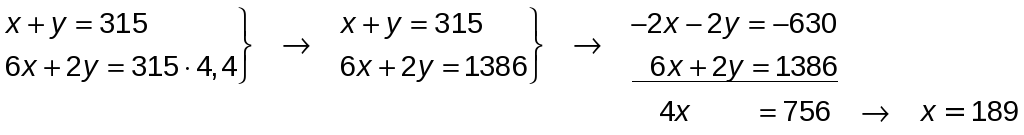
Luego, y = 315 − 189 = 126.
Ha de mezclar 189 l de vino bueno con 126 l del más corriente.
Ejercicio nº 9.-
a) Resuelve la siguiente inecuación y escribe la solución en forma de intervalo:
![]()
b) Resuelve la siguiente inecuación estudiando el signo de cada factor:
![]()
Solución:
![]()
La solución en forma de intervalo será: (−∞, −2)
b) El factor 5 − x = 0 si x = 5, y el factor x + 3 = 0, si x = −3.
Así:
![]()
Gráficamente:

Para que un producto de dos factores sea mayor que 0, ambos han de tener el mismo signo, luego la solución será el intervalo (−3, 5).
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
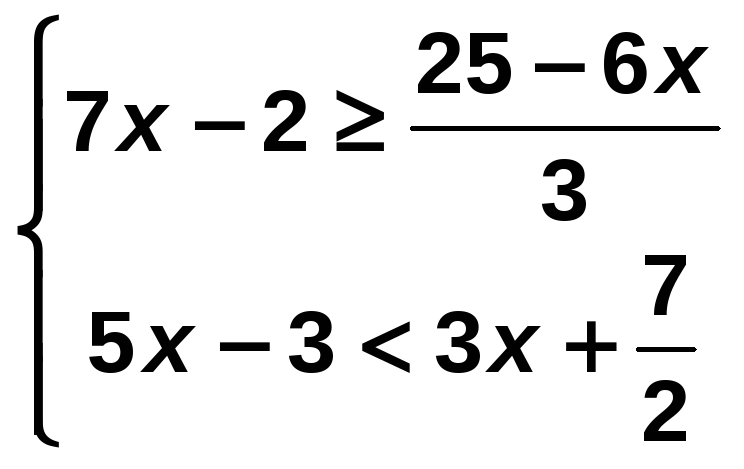
Solución:
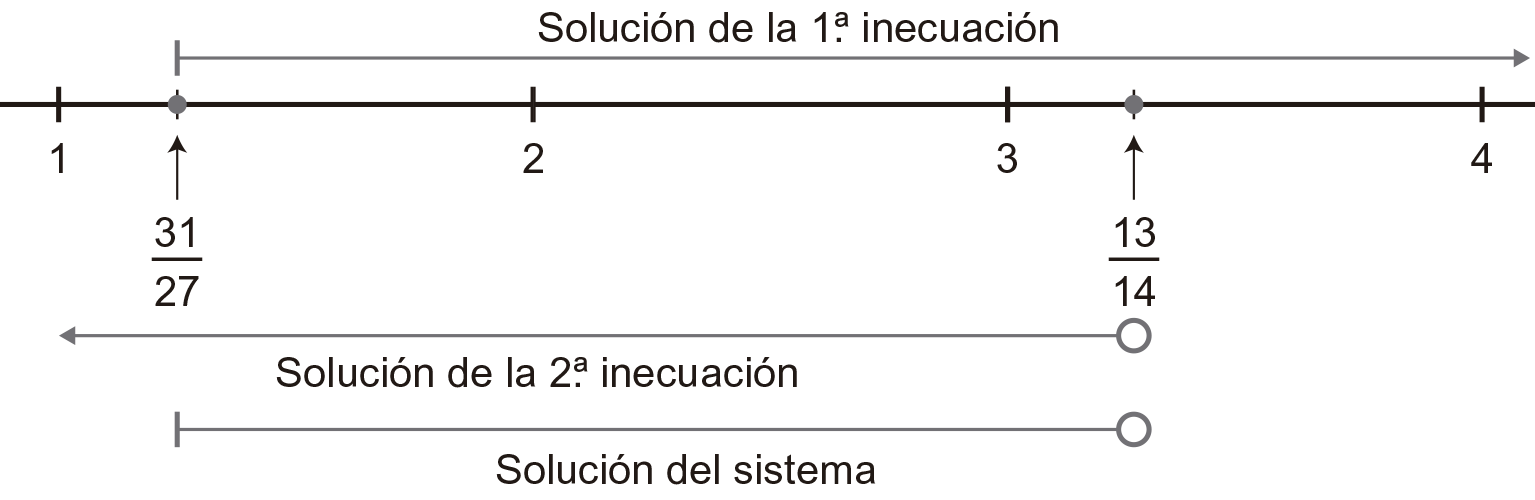
Resolvemos cada inecuación por separado y buscamos la solución que sea común a ambas:
![]()
![]()
![]()
Ejercicio nº 11.-
a) Un grupo de 6 personas han desayunado (café + bollería) pagando entre todos poco más de 10 €. ¿Qué puedes decir del precio de cada desayuno?
b) Al día siguiente, en ese mismo sitio, desayunaron 8 personas y les cuesta menos de 14 €. ¿Cuánto crees que costará el desayuno?
Solución:
![]()
El precio de cada desayuno supera los 1,66 €.

Uniendo ambos apartados deducimos que 1,66 x 1,75; luego es de suponer que el precio del desayuno será, más o menos, de 1,70 €.
Ejercicio nº 12.-
Calcula los valores que ha de tomar k para que la ecuación x2 − 6x + k = 0 tenga:
a) Dos soluciones iguales.
b) Dos soluciones que no sean números reales.
Solución:
a) Tendrá dos soluciones iguales cuando b2− 4ac = 0, es decir,
(−6)2− 4k = 0 → 36 − 4k = 0 → k = 9
b) Que las soluciones no sean números reales equivale a decir que la ecuación no tenga solución en el campo de los números reales; esto ocurre cuando b2− 4ac < 0.
36 − 4k < 0 → 36 < 4k → k > 9
Ejercicio nº 13.-
Resuelve:
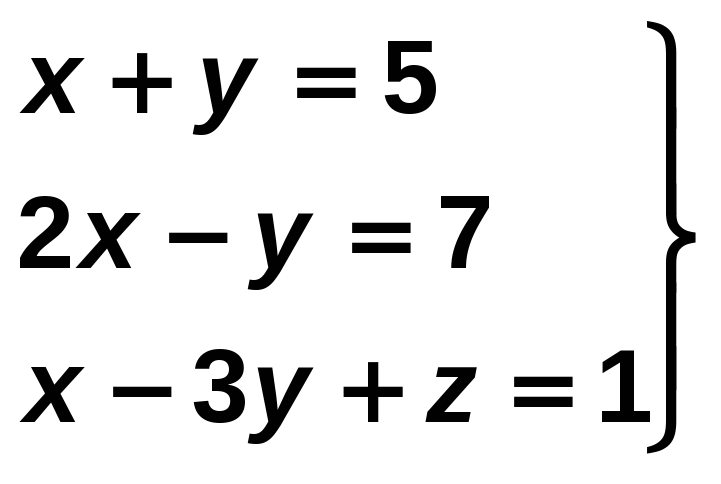
Solución:
Resolvemos el sistema formado por las dos primeras ecuaciones:
![]()
![]()
Sustituyendo x = 4, y = 1 en la tercera ecuación obtenemos z :
x − 3y + z = −1 → 4 − 3 · 1 + z = −1 → 4 − 3 + z = −1 → z = −2
La solución del sistema es x = 4, y = 1, z = −2.
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | D |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve:
![]()
![]()
Solución:
![]()
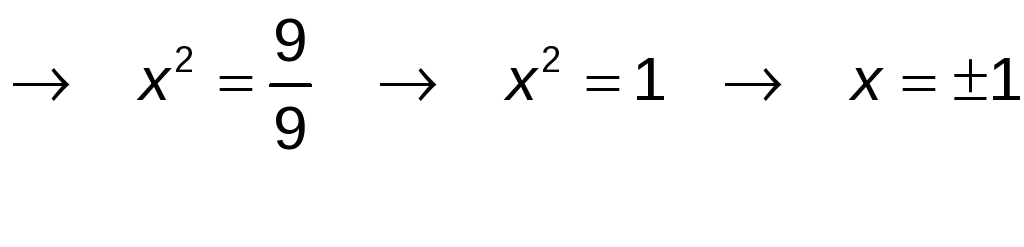
Las soluciones son x1= 1 y x2=−1.
b) Ecuación bicuadrada; hacemos x2= z y obtenemos:
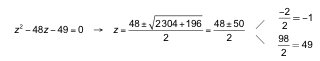
![]()
Las soluciones son x1= 7 y x2= −7.
Ejercicio nº 2.-
Resuelve las ecuaciones:
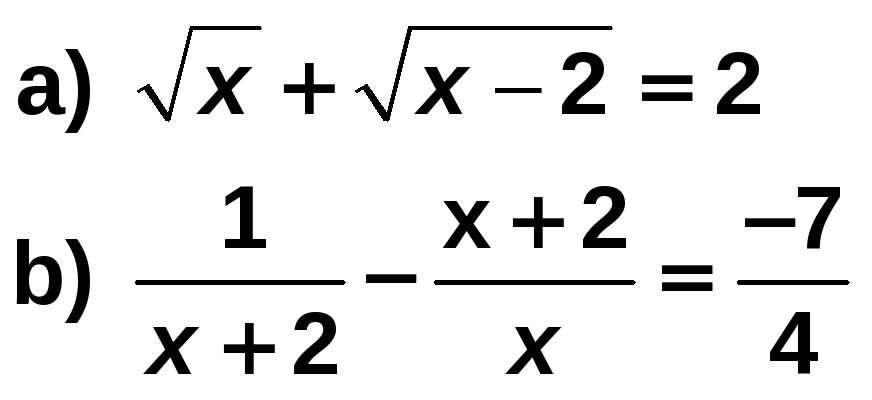
Solución:
![]()
Elevamos al cuadrado ambos miembros:
![]()
Volvemos a elevar al cuadrado:
![]()
Lo comprobamos:
![]()
![]()
b) Multiplicamos ambos miembros por 4x(x + 2):
![]()
![]()
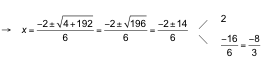
Comprobamos estas soluciones sobre la ecuación:
![]()
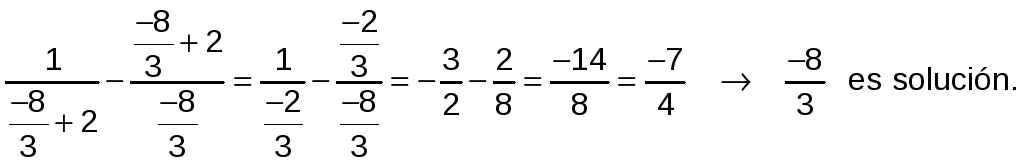
![]()
Ejercicio nº 3.-
![]()
![]()
Solución:
Tenemos un producto de factores igualado a 0, luego se ha de cumplir:
x = 0
![]()
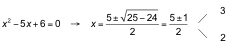
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
![]()
b) 2log x = log (15 ‒ 2x)
Solución:
![]()
→ 23x+ 26x= 4 160
Hacemos un cambio de variable: t = 23x
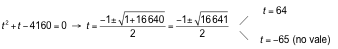
64 = 23x→ 26= 23x→ x = 2
b) 2log x = log (15 ‒ 2x) → log x2= log (15 ‒ 2x) → x2= 15 ‒ 2x →
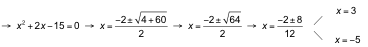
La solución válida es x = 3, puesto que, log (‒5) no existe.
Ejercicio nº 5.-
El área de un rombo es de 240 cm2. Calcula la longitud de las diagonales sabiendo que suman 46 cm.
Solución:
Llamamos x y 46 − x a las longitudes de ambas diagonales.
![]()
Así:
![]()
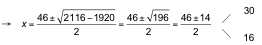
![]()
Luego, la longitud de las diagonales es de 16 cm y 30 cm.
Ejercicio nº 6.-
Resuelve el sistema:
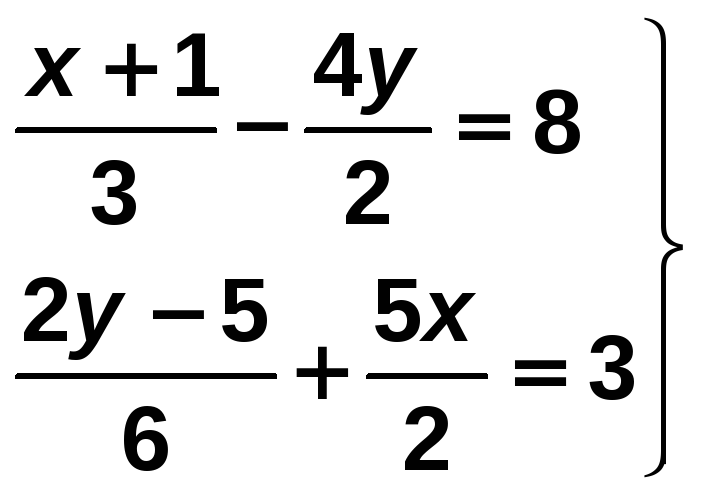
Solución:
Comenzamos por simplificar cada una de las ecuaciones del sistema:
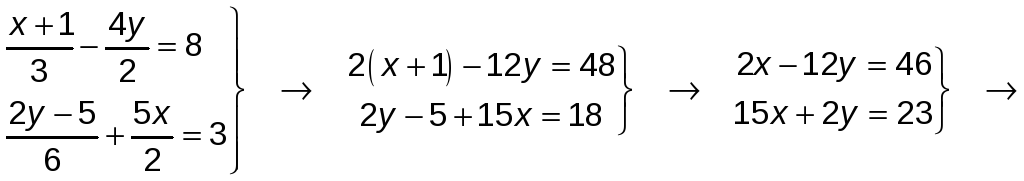
![]()
Despejamos x de la primera ecuación y sustituimos en la segunda:
x = 23 + 6y
![]()
![]()
Calculamos el valor de x :
![]()
Comprobamos con la calculadora:
2 − 6 × 7 ab/c 2 +/− = 23
15 × 2 + 2 × 7 ab/c 2 +/− = 23
Ejercicio nº 7.-
Halla la solución del siguiente sistema de ecuaciones:
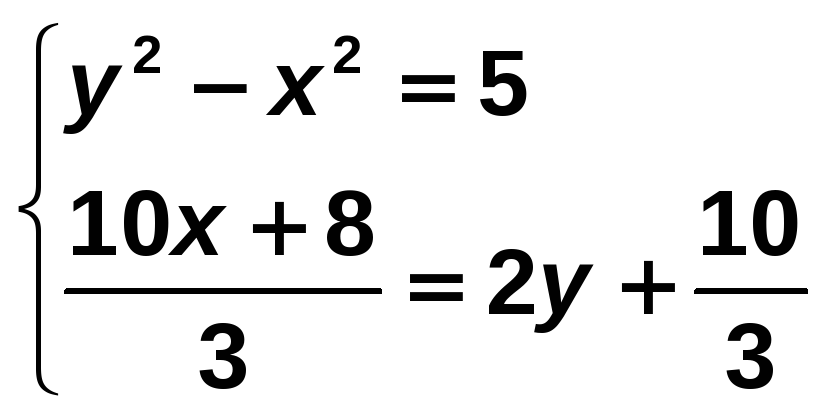
Solución:
Transformamos la segunda ecuación en una equivalente sin denominadores:
![]()
El sistema a resolver es:
![]()
Despejamos x de la segunda ecuación y sustituimos en la primera:
![]()
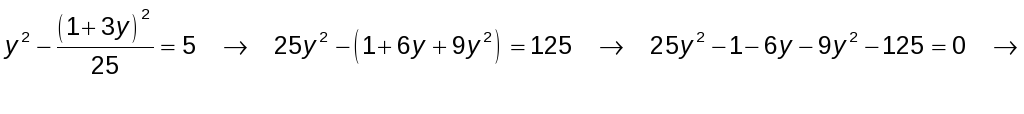
![]()
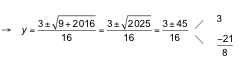
![]()
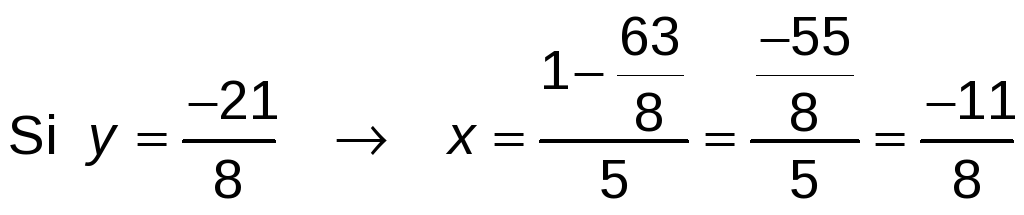
Las soluciones al sistema son:
Ejercicio nº 8.-
Pablo compró un equipo de música y un reproductor de DVD por 870 €. Después de algún tiempo, los vende por 770,50 €. Con el equipo de música perdió el 10% de su valor y con el reproductor de DVD el 15%. ¿Cuánto le costó cada uno?
Solución:
Llamamos:
x = “precio inicial del equipo de música”
y = “precio inicial del reproductor de DVD”
![]()
Aplicamos el método de sustitución:
x = 870 − y
0,90 (870 − y) + 0,85y = 770,50 → 783 − 0,90y + 0,85y = 770,50 → −0,05y = −12,5 → → y = 250
x = 870 − y → x = 870 − 250 = 620
El equipo de música costó 620 € y el reproductor de DVD 250 €.
Ejercicio nº 9.-
a) Halla el conjunto de soluciones de la inecuación y escribe la solución en forma de intervalo:
![]()
b) Halla el conjunto de soluciones de la inecuación:
![]()
Solución:
a) Multiplicamos la inecuación por 3, quitamos paréntesis y agrupamos los términos como en las ecuaciones:
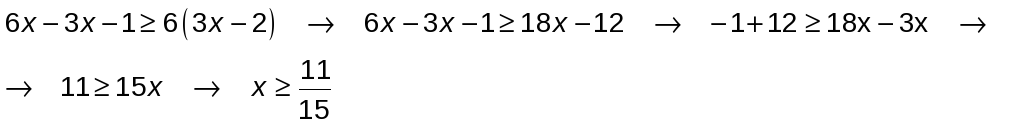
![]()
b) Reducimos a una ecuación de segundo grado y calculamos sus soluciones:
![]()
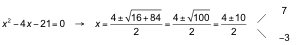
![]()
Estudiemos entonces el signo de cada factor:

Para que un producto de dos factores sea positivo, ambos factores han de tener el mismo signo.
![]()
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
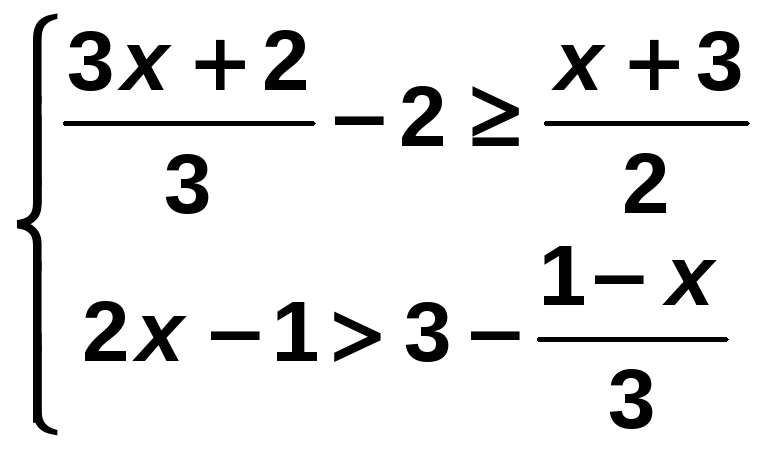
Solución:
Resolvemos cada inecuación y buscamos las soluciones comunes:
![]()
![]()
![]()

Ejercicio nº 11.-
Un fabricante de bombillas obtiene un beneficio de 0,80 € por cada pieza que sale de su taller para la venta pero sufre una pérdida de 1 € por cada pieza defectuosa que debe retirar.
En un día quiere fabricar 2 250 bombillas para obtener al menos un beneficio de 1 710 €. ¿Cuántas bombillas han de ser válidas?
Solución:
Llamamos:
x = “nº de bombillas válidas” → beneficio = 0,80x
2 250 − x = “nº de bombillas defectuosas” → pérdida = 1·(2 250 − x) = 2 250 − x
Se busca que el beneficio final sea mayor o igual que 1 710 € .
0,80x − 2 250 + x ≥ 1 710 → 1,80x ≥ 3 960 → x ≥ 2 200
Han de ser válidas por lo menos 2 200 bombillas.
Ejercicio nº 12.-
Escribe un sistema no lineal de dos ecuaciones con dos incógnitas que tenga como solución x = 3, y = −2. ¿Sería la única solución del sistema?
Solución:
Por ejemplo:
![]()
Otra solución de este sistema sería x = −2, y = 3.
Ejercicio nº 13.-
Resuelve el sistema:
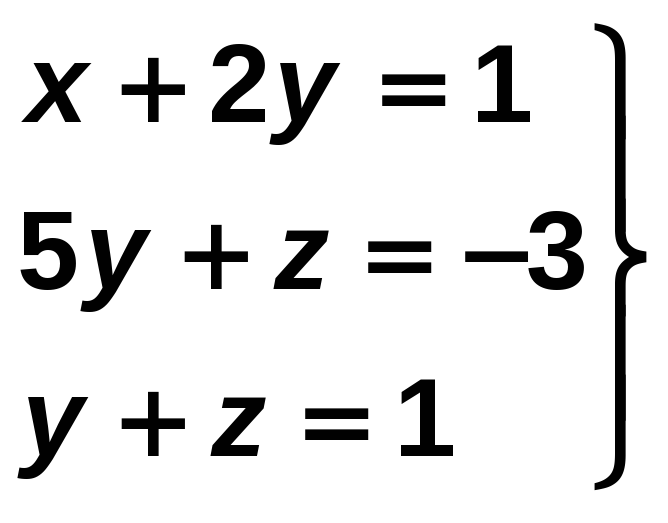
Solución:
Resolvemos el sistema formado por las dos últimas ecuaciones:
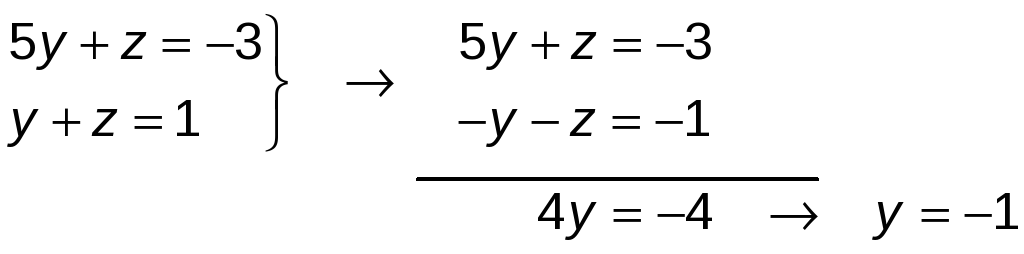
y + z = 1 → −1 + z = 1 → z = 2
Sustituyendo y = −1 en la primera ecuación, calculamos el valor de x:
x + 2 · (−1) = 1 → x − 2 = 1 → x = 3
La solución del sistema es x = 3, y = −1, z = 2.
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | E |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve:
![]()
Solución:
a) Efectuamos los paréntesis teniendo en cuenta que todos son productos notables:
![]()
![]()
![]()
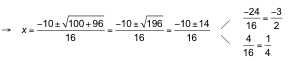
![]()
b) Ecuación bicuadrada en la que podemos extraer x 2 como factor común:
![]()
Así:
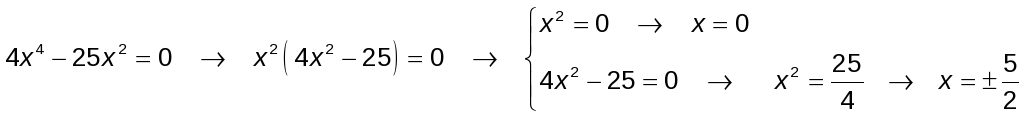
![]()
Ejercicio nº 2.-
Resuelve las siguientes ecuaciones:
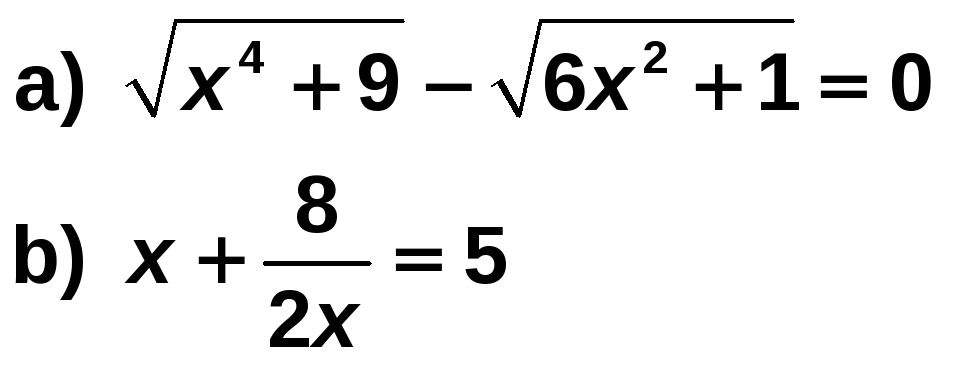
Solución:
![]()
Elevamos ambos miembros al cuadrado:
![]()
Ecuación bicuadrada, que resolvemos haciendo el cambio x 2= z :
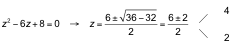
![]()
Comprobación:
![]()
![]()
b) Multiplicamos ambos miembros por 2x:
![]()
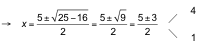
Comprobación de las posibles soluciones:
![]()
![]()
Las soluciones son x1= 4 y x2= 1.
Ejercicio nº 3.-
![]()
Solución:
Para que el producto de varios factores sea 0, alguno de ellos tiene que ser 0. Así:
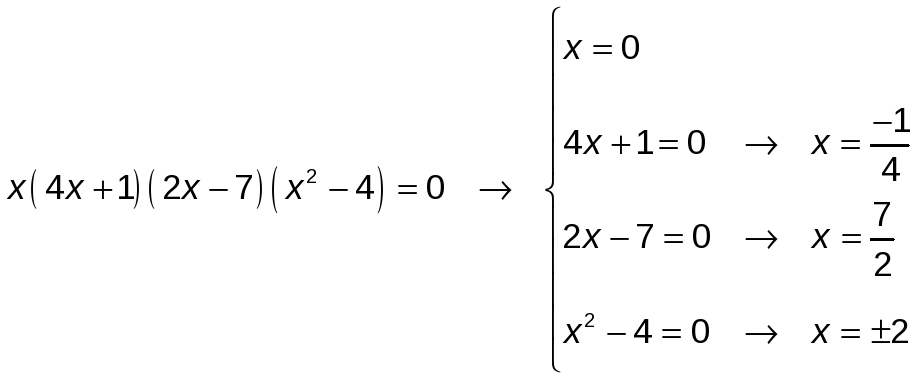
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
a) 3x + 3x + 1 ‒ 3x ‒ 1 = 297
b) log 3x + log 40 = 2
Solución:
![]()
Cambio de variable: 3x= t
![]()
→ 3x= 81 → 3x= 34→ x = 4
b) log 3x + log 40 = 2
log (3x · 40) = log 100 → 3x · 40 = 100 → 120x = 100 →
![]()
Ejercicio nº 5.-
La base de un rectángulo mide 3 cm más que la altura. Si aumentamos la base en 2 cm y la altura en 3 cm, la superficie del nuevo rectángulo es el doble de la superficie del inicial.
Calcula las dimensiones del rectángulo inicial.
Solución:
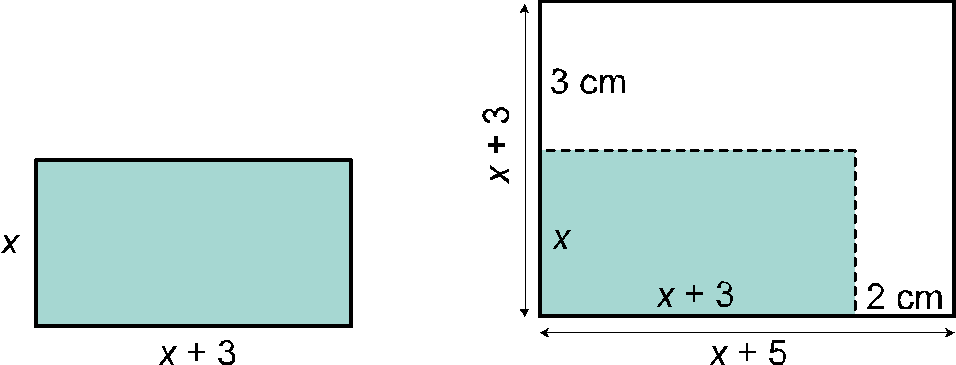
![]()
![]()
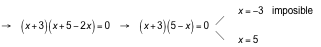
Las dimensiones del rectángulo inicial son 5 cm y 8 cm.
Ejercicio nº 6.-
Resuelve el siguiente sistema por el método que consideres más adecuado:
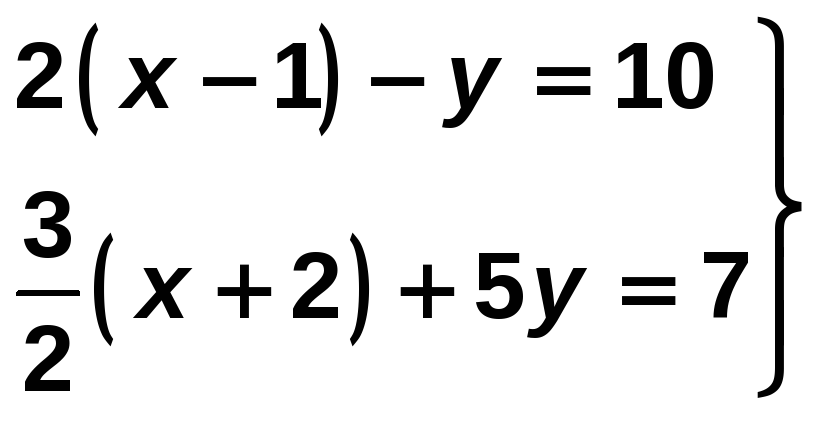
Solución:
Comenzamos por simplificar cada una de las ecuaciones del sistema:
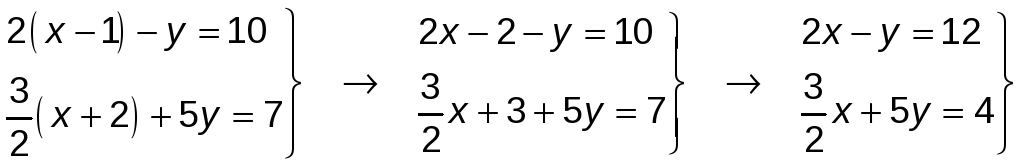
Método de sustitución → Despejamos y de la primera ecuación y sustituimos en la segunda:
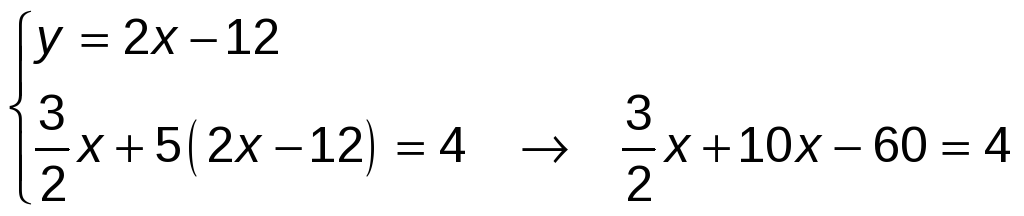
Multiplicamos ambos miembros de la ecuación por 2:
![]()
Se calcula el valor de y :
![]()
Comprobamos con la calculadora:
2 × [128 ab/c 23 − 1] − [20 ab/c 23 +/− ] = 10
3ab/c 2 × [128 ab/c 23 + 2] + 5 × 20 ab/c 23 +/− = 7
Ejercicio nº 7.-
Halla la solución del sistema:
![]()
Solución:
Multiplicamos la segunda ecuación por −3 para aplicar el método de reducción:
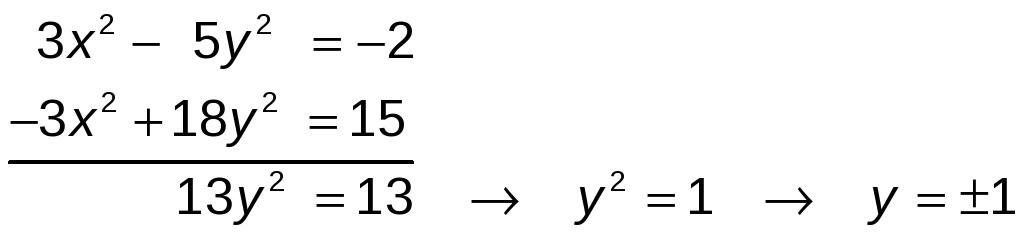
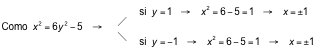
Las soluciones son:
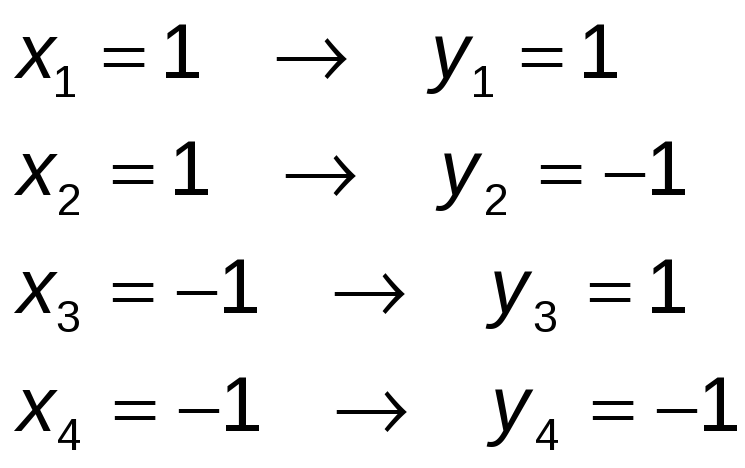
Ejercicio nº 8.-
El área de un jardín rectangular mide 900 m2 y está rodeado por un paseo de 5 m de ancho, cuya área es de 850 m2. Calcula las dimensiones del jardín.
Solución:
Llamamos x, y a las dimensiones del jardín.
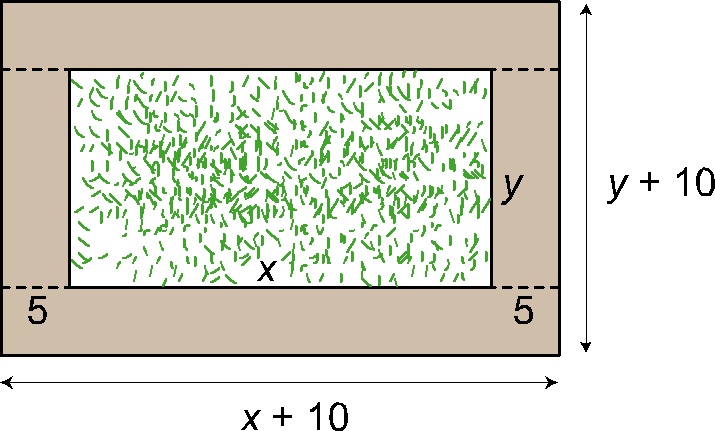
La zona sombreada es el paseo que está formado por dos rectángulos de cada uno de los siguientes tipos:
![]()
![]()
![]()
![]()
Área del paseo = 850 → 2S1 + 2S2 = 850 → S1 + S2 = 425 →
→ 5x + 50 + 5y = 425 → 5x + 5y = 375 → x + y = 75
El sistema que resuelve el problema es:
![]()
Despejamos x de la 2ª ecuación y sustituimos en la primera:
x = 75 − y
y (75 − y) = 900 → y2− 75y + 900 = 0 →
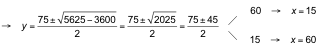
Las dimensiones del jardín son 15 m y 60 m.
Ejercicio nº 9.-
a) Resuelve gráficamente la inecuación, expresando la solución en forma de intervalo:
![]()
b) Halla el conjunto de soluciones de la inecuación:
x2 + 3x ‒ 6 > 8 ‒ 2x
Solución:
![]()
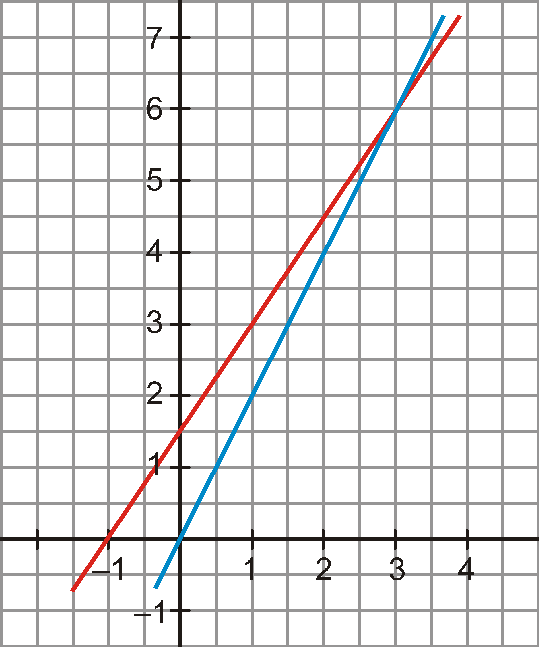

b) x2+ 3x ‒ 6 > 8 ‒ 2x → x2+ 5x ‒ 14 > 0
Resolvemos la ecuación x2+ 5x ‒ 14 = 0:
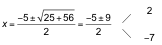
Estudiamos el signo de x2+ 5x − 14 según los valores que damos a x.
Los valores −7 y 2 dividen la recta real en tres partes, en cada una de las cuales estudiaremos el signo de x2+ 5x − 14.
![]()
![]()
![]()
![]()
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
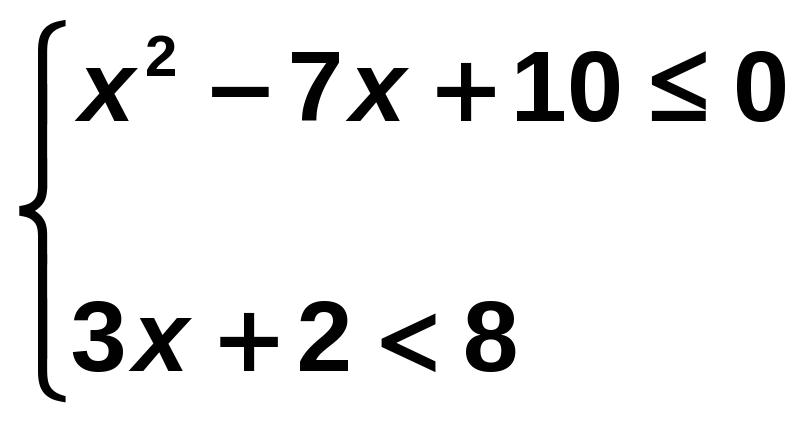
Solución:
Resolvemos independientemente cada inecuación y buscamos las soluciones comunes:
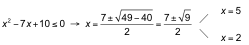

La solución de esta inecuación es [2, 5].
3x + 2 < 8 → 3x < 6 → x < 2
Este sistema de inecuación no tiene solución.

Ejercicio nº 11.-
El producto de dos números enteros consecutivos es menor que 6. ¿Cuáles pueden ser esos números?
Solución:
Dos números consecutivos son x, x + 1.
x(x + 1) < 6 → x2+ x < 6 → x2+ x − 6 < 0
Resolvemos la inecuación buscando las raíces de x2+ x − 6.
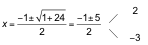
Estudiamos el signo de x2+ x − 6 en cada uno de los siguientes intervalos:
(−∞, −3) → (−4)2 − 4 − 6 > 0
(−3, 2) → 02+ 0 − 6 < 0
(2, +∞) → 32+ 3 − 6 > 0
La solución de la inecuación x2+ x − 6 < 0 es (−3, 2); por tanto los números enteros consecutivos pueden ser −2 y −1, −1 y 0, 0 y 1, 1 y 2.
Ejercicio nº 12.-
![]()
Solución:
![]()
![]()
Buscamos la otra solución de la ecuación 2x2− 9x − 5 = 0.
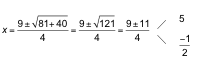
La otra solución es x = 5.
Ejercicio nº 13.-
Un tractor sube un camino montañoso a 30 km/h y lo baja a 50 km/h. Calcula la velocidad media del recorrido.
Solución:
Hacemos un cuadro para organizar los datos y ayudarnos en el planteamiento del problema.
-
DISTANCIA (km)
VELOCIDAD
TIEMPO (h)
SUBIDA
d
30 km/h
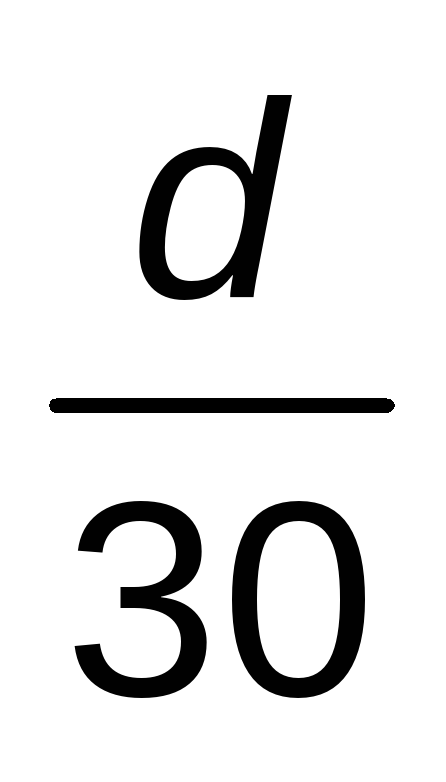
BAJADA
d
50 km/h
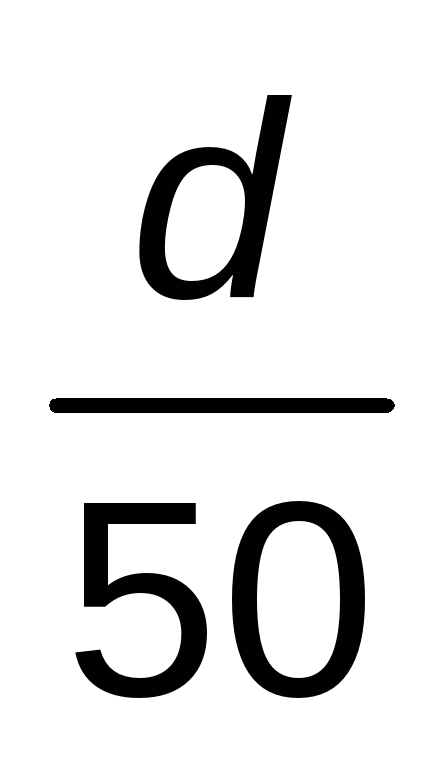
TOTAL RECORRIDO
2d
x
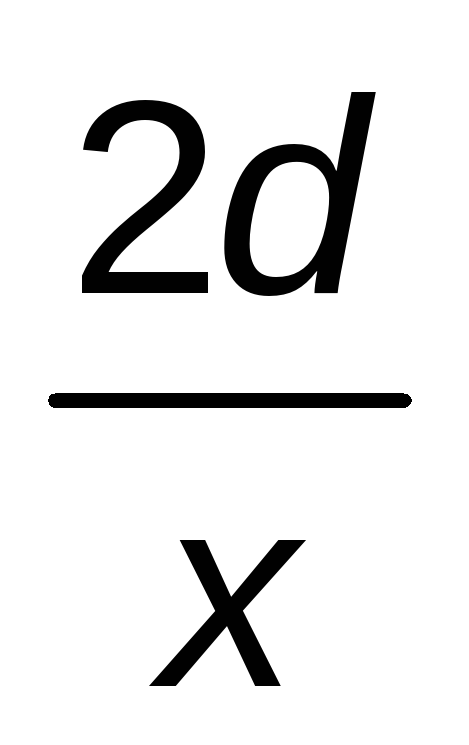
Por tanto:
![]()
Dividiendo entre d:
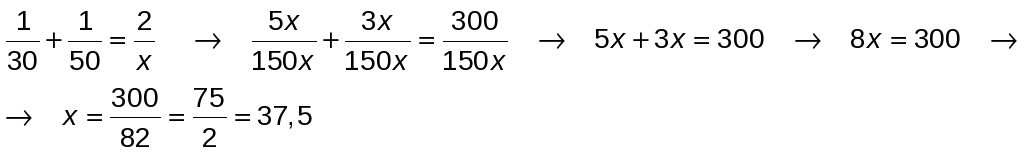
La velocidad media del recorrido ha sido de 37,5 km/h.
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | F |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve:
![]()
![]()
Solución:
![]()
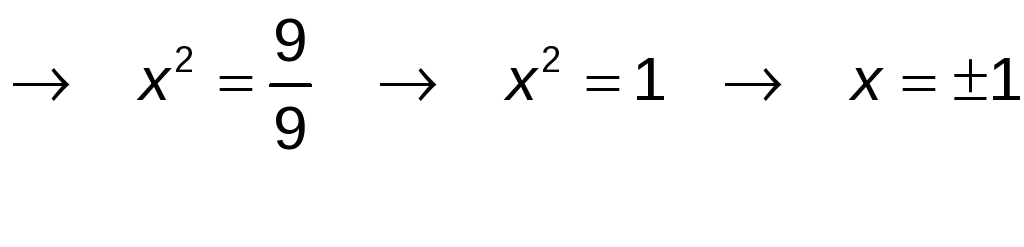
Las soluciones son x1= 1 y x2=−1.
b) Ecuación bicuadrada; hacemos x2= z y obtenemos:
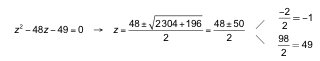
![]()
Las soluciones son x1= 7 y x2= −7.
Ejercicio nº 2.-
Resuelve:
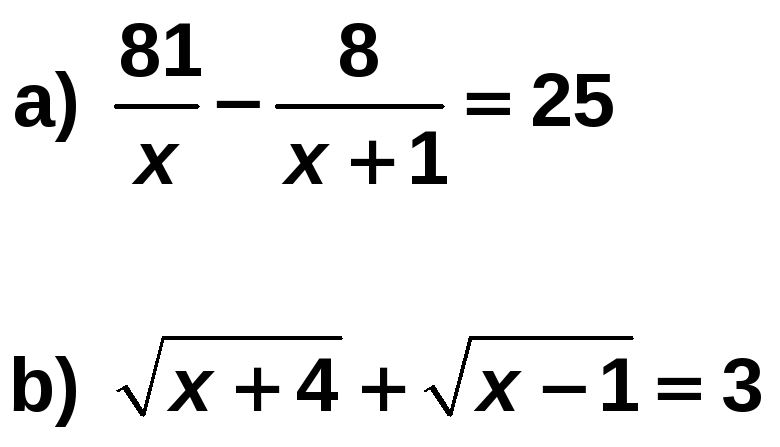
Solución:
a) Multiplicamos ambos miembros por x (x + 1):
![]()
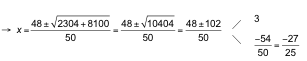
Comprobamos si son, o no, solución en la ecuación inicial:
![]()
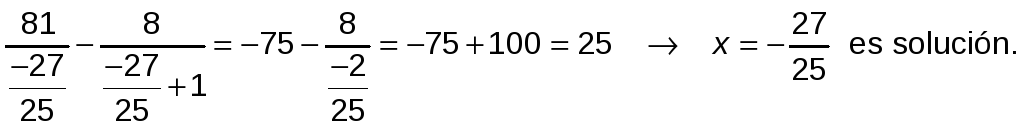
![]()
![]()
Elevamos ambos miembros al cuadrado:
![]()
Volvemos a elevar al cuadrado:
![]()
Comprobamos si es, o no, solución:
![]()
![]()
![]()
Ejercicio nº 3.-
![]()
![]()
Solución:
Tenemos un producto de factores igualado a 0, luego se ha de cumplir:
x = 0
![]()
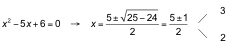
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
![]()
b) 2log x = log (15 ‒ 2x)
Solución:
![]()
→ 23x+ 26x= 4 160
Hacemos un cambio de variable: t = 23x
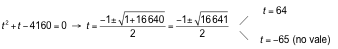
64 = 23x→ 26= 23x→ x = 2
b) 2log x = log (15 ‒ 2x) → log x2= log (15 ‒ 2x) → x2= 15 ‒ 2x →
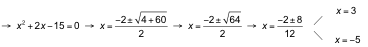
La solución válida es x = 3, puesto que, log (‒5) no existe.
Ejercicio nº 5.-
![]()
en reformar la casa, el 10% de la cantidad inicial en ropa y el resto, 260 €, los ahorró. ¿Cuánto dinero heredó?
Solución:
x = "dinero heredado"

La ecuación que resuelve el problema será:
![]()
Multiplicamos ambos miembros por 30:
![]()
![]()
Ejercicio nº 6.-
Resuelve por el método que consideres más apropiado y comprueba la solución obtenida en el siguiente sistema:
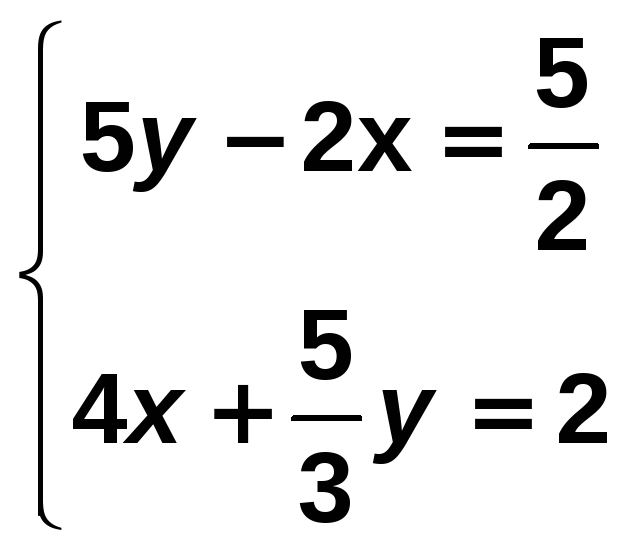
Solución:
Utilizamos el método de reducción en y ; para ello multiplicamos la 2ª ecuación por −3:
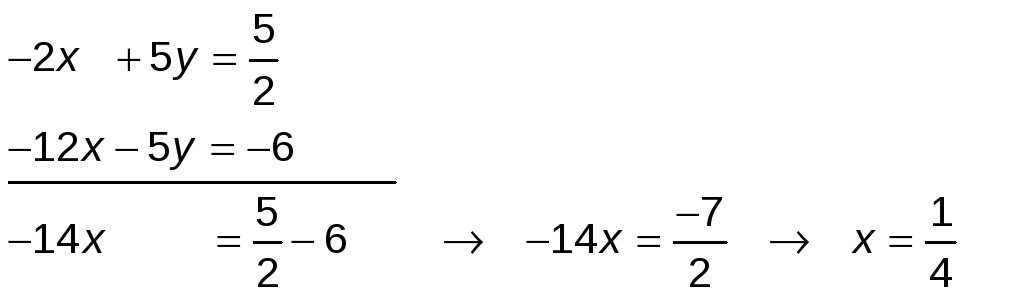
Calculamos y sustituimos el valor de x en la 1ª ecuación:
![]()
![]()
Comprobamos la solución:
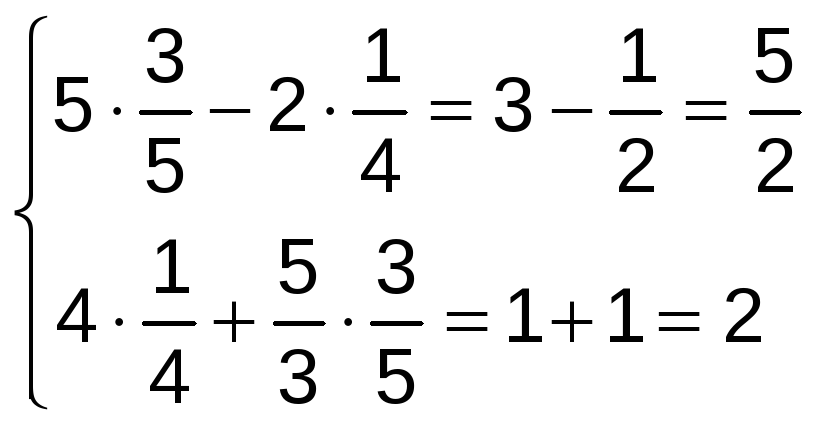
Ejercicio nº 7.-
Resuelve:
![]()
Solución:
![]()
Aplicamos el método de igualación:
![]()
Elevamos al cuadrado los dos miembros de la última igualdad:
![]()
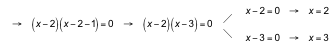
![]()
Comprobamos las soluciones sobre el sistema:
![]()
![]()
Ejercicio nº 8.-
Pablo compró un equipo de música y un reproductor de DVD por 870 €. Después de algún tiempo, los vende por 770,50 €. Con el equipo de música perdió el 10% de su valor y con el reproductor de DVD el 15%. ¿Cuánto le costó cada uno?
Solución:
Llamamos:
x = “precio inicial del equipo de música”
y = “precio inicial del reproductor de DVD”
![]()
Aplicamos el método de sustitución:
x = 870 − y
0,90 (870 − y) + 0,85y = 770,50 → 783 − 0,90y + 0,85y = 770,50 → −0,05y = −12,5 → → y = 250
x = 870 − y → x = 870 − 250 = 620
El equipo de música costó 620 € y el reproductor de DVD 250 €.
Ejercicio nº 9.-
a) Resuelve gráficamente la inecuación, expresando la solución en forma de intervalo:
![]()
b) Halla el conjunto de soluciones de la inecuación:
x2 + 3x ‒ 6 > 8 ‒ 2x
Solución:
![]()


b) x2+ 3x ‒ 6 > 8 ‒ 2x → x2+ 5x ‒ 14 > 0
Resolvemos la ecuación x2+ 5x ‒ 14 = 0:
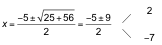
Estudiamos el signo de x2+ 5x − 14 según los valores que damos a x.
Los valores −7 y 2 dividen la recta real en tres partes, en cada una de las cuales estudiaremos el signo de x2+ 5x − 14.
![]()
![]()
![]()
![]()
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
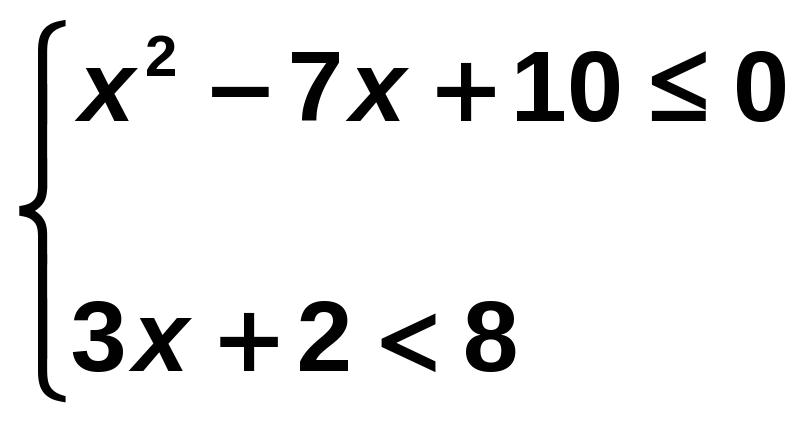
Solución:
Resolvemos independientemente cada inecuación y buscamos las soluciones comunes:
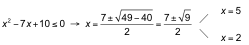

La solución de esta inecuación es [2, 5].
3x + 2 < 8 → 3x < 6 → x < 2
Este sistema de inecuación no tiene solución.

Ejercicio nº 11.-
En un triángulo isósceles el lado desigual es la mitad de los lados iguales.
a) Para que el perímetro no supere los 30 cm, ¿qué puedes deducir de la longitud de los lados?
b) ¿Y si además buscamos un perímetro al menos de 15 cm?
Solución:
![]()
![]()
![]()
Los lados iguales no deben superar los 12 cm y el lado desigual ha de ser menor o igual
![]()
![]()
![]()
Luego uniendo ambos apartados llegamos a la siguiente conclusión:
− Los lados iguales, x, miden como mínimo 6 cm y como máximo 12 cm (6 ≤ x ≤ 12).
![]()
Ejercicio nº 12.-
Calcula los valores que ha de tomar k para que la ecuación x2 − 6x + k = 0 tenga:
a) Dos soluciones iguales.
b) Dos soluciones que no sean números reales.
Solución:
a) Tendrá dos soluciones iguales cuando b2− 4ac = 0, es decir,
(−6)2− 4k = 0 → 36 − 4k = 0 → k = 9
b) Que las soluciones no sean números reales equivale a decir que la ecuación no tenga solución en el campo de los números reales; esto ocurre cuando b2− 4ac < 0.
36 − 4k < 0 → 36 < 4k → k > 9
Ejercicio nº 13.-
Un tractor sube un camino montañoso a 30 km/h y lo baja a 50 km/h. Calcula la velocidad media del recorrido.
Solución:
Hacemos un cuadro para organizar los datos y ayudarnos en el planteamiento del problema.
-
DISTANCIA (km)
VELOCIDAD
TIEMPO (h)
SUBIDA
d
30 km/h
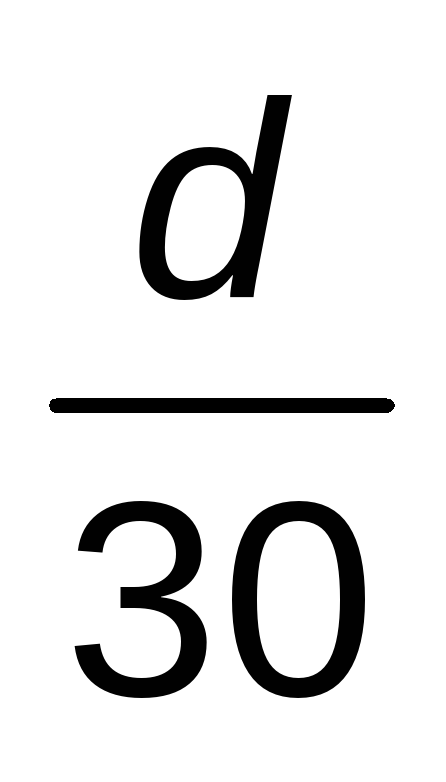
BAJADA
d
50 km/h
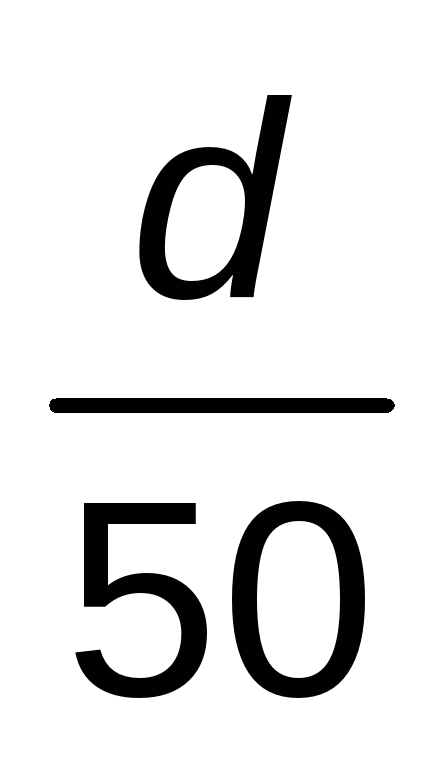
TOTAL RECORRIDO
2d
x
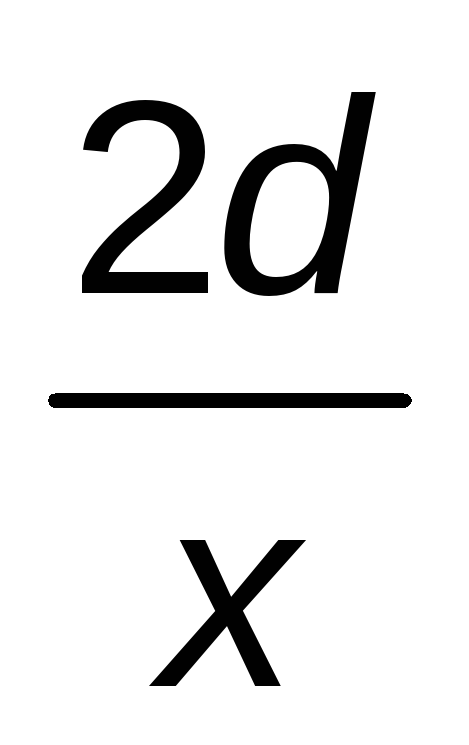
Por tanto:
![]()
Dividiendo entre d:
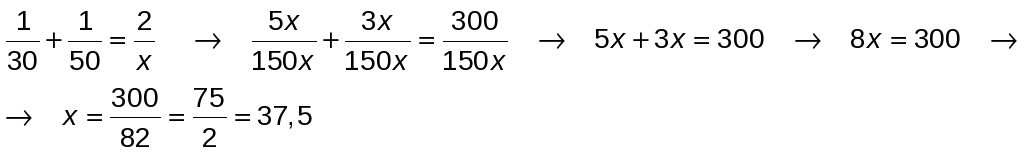
La velocidad media del recorrido ha sido de 37,5 km/h.







