| Indice del artículo |
|---|
| ECUACIONES , INECUACIONES Y SISTEMAS. |
| Examen2 |
| EXAMEN 3 |
| EXAMEN 4 |
| EXAMEN 5 |
| EXAMEN 6 |
| Todas las páginas |
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | D |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve:
![]()
![]()
Solución:
![]()
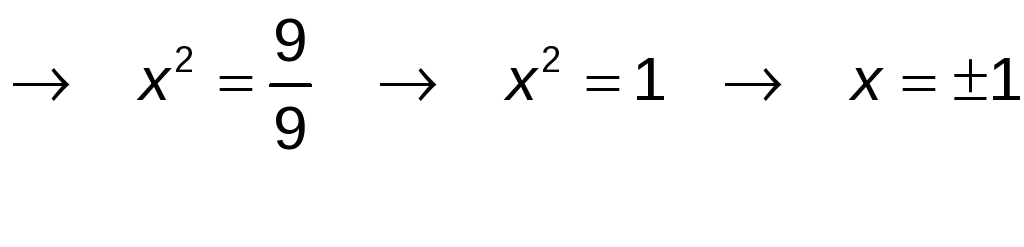
Las soluciones son x1= 1 y x2=−1.
b) Ecuación bicuadrada; hacemos x2= z y obtenemos:
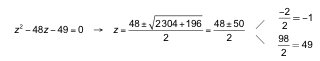
![]()
Las soluciones son x1= 7 y x2= −7.
Ejercicio nº 2.-
Resuelve las ecuaciones:
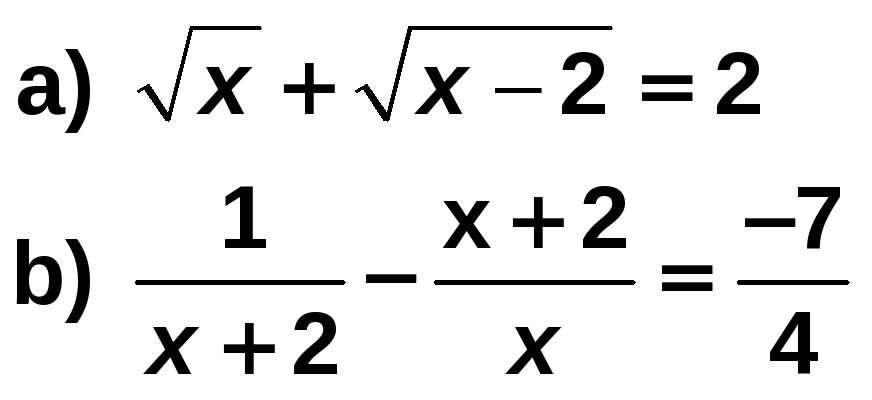
Solución:
![]()
Elevamos al cuadrado ambos miembros:
![]()
Volvemos a elevar al cuadrado:
![]()
Lo comprobamos:
![]()
![]()
b) Multiplicamos ambos miembros por 4x(x + 2):
![]()
![]()
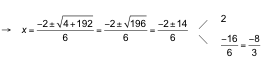
Comprobamos estas soluciones sobre la ecuación:
![]()
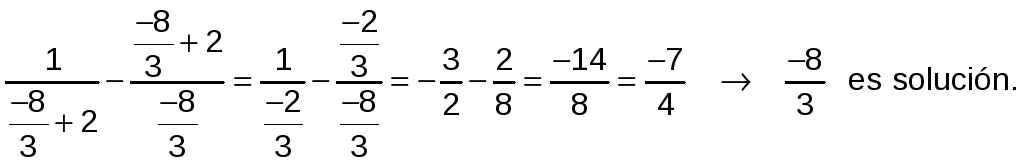
![]()
Ejercicio nº 3.-
![]()
![]()
Solución:
Tenemos un producto de factores igualado a 0, luego se ha de cumplir:
x = 0
![]()
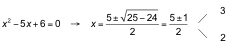
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
![]()
b) 2log x = log (15 ‒ 2x)
Solución:
![]()
→ 23x+ 26x= 4 160
Hacemos un cambio de variable: t = 23x
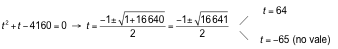
64 = 23x→ 26= 23x→ x = 2
b) 2log x = log (15 ‒ 2x) → log x2= log (15 ‒ 2x) → x2= 15 ‒ 2x →
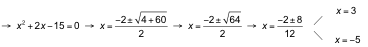
La solución válida es x = 3, puesto que, log (‒5) no existe.
Ejercicio nº 5.-
El área de un rombo es de 240 cm2. Calcula la longitud de las diagonales sabiendo que suman 46 cm.
Solución:
Llamamos x y 46 − x a las longitudes de ambas diagonales.
![]()
Así:
![]()
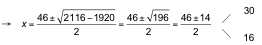
![]()
Luego, la longitud de las diagonales es de 16 cm y 30 cm.
Ejercicio nº 6.-
Resuelve el sistema:
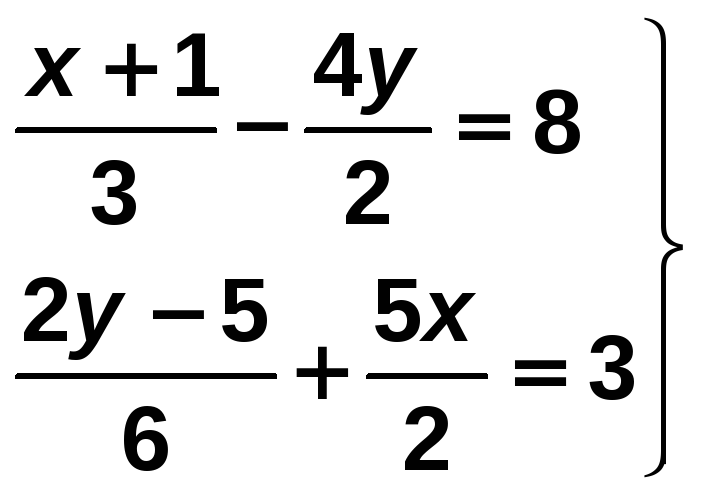
Solución:
Comenzamos por simplificar cada una de las ecuaciones del sistema:
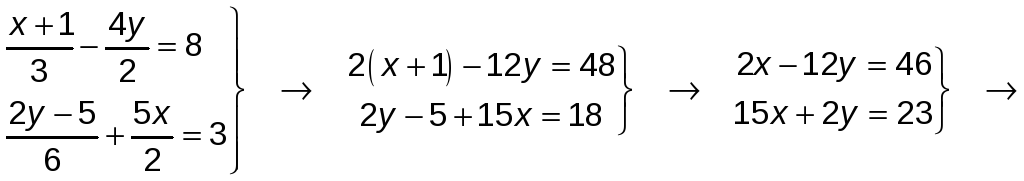
![]()
Despejamos x de la primera ecuación y sustituimos en la segunda:
x = 23 + 6y
![]()
![]()
Calculamos el valor de x :
![]()
Comprobamos con la calculadora:
2 − 6 × 7 ab/c 2 +/− = 23
15 × 2 + 2 × 7 ab/c 2 +/− = 23
Ejercicio nº 7.-
Halla la solución del siguiente sistema de ecuaciones:
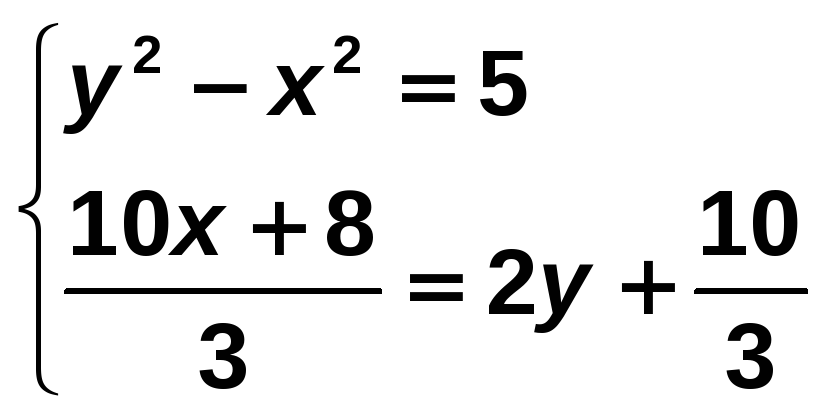
Solución:
Transformamos la segunda ecuación en una equivalente sin denominadores:
![]()
El sistema a resolver es:
![]()
Despejamos x de la segunda ecuación y sustituimos en la primera:
![]()
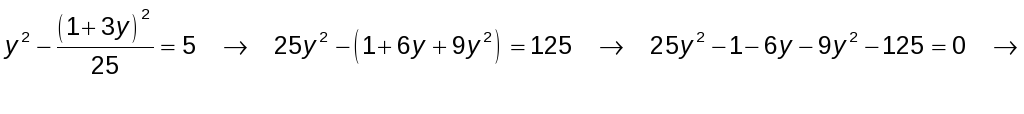
![]()
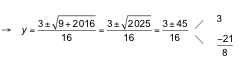
![]()
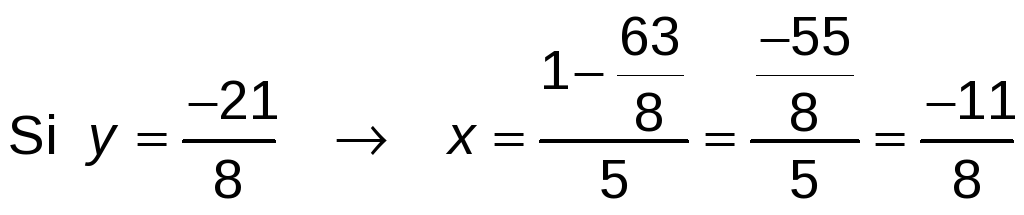
Las soluciones al sistema son:
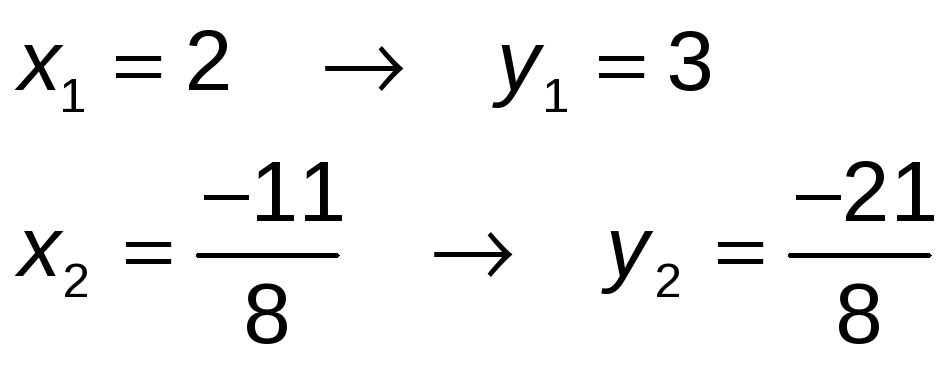
Ejercicio nº 8.-
Pablo compró un equipo de música y un reproductor de DVD por 870 €. Después de algún tiempo, los vende por 770,50 €. Con el equipo de música perdió el 10% de su valor y con el reproductor de DVD el 15%. ¿Cuánto le costó cada uno?
Solución:
Llamamos:
x = “precio inicial del equipo de música”
y = “precio inicial del reproductor de DVD”
![]()
Aplicamos el método de sustitución:
x = 870 − y
0,90 (870 − y) + 0,85y = 770,50 → 783 − 0,90y + 0,85y = 770,50 → −0,05y = −12,5 → → y = 250
x = 870 − y → x = 870 − 250 = 620
El equipo de música costó 620 € y el reproductor de DVD 250 €.
Ejercicio nº 9.-
a) Halla el conjunto de soluciones de la inecuación y escribe la solución en forma de intervalo:
![]()
b) Halla el conjunto de soluciones de la inecuación:
![]()
Solución:
a) Multiplicamos la inecuación por 3, quitamos paréntesis y agrupamos los términos como en las ecuaciones:
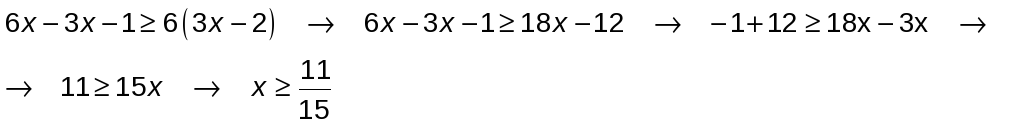
![]()
b) Reducimos a una ecuación de segundo grado y calculamos sus soluciones:
![]()
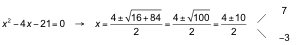
![]()
Estudiemos entonces el signo de cada factor:

Para que un producto de dos factores sea positivo, ambos factores han de tener el mismo signo.
![]()
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
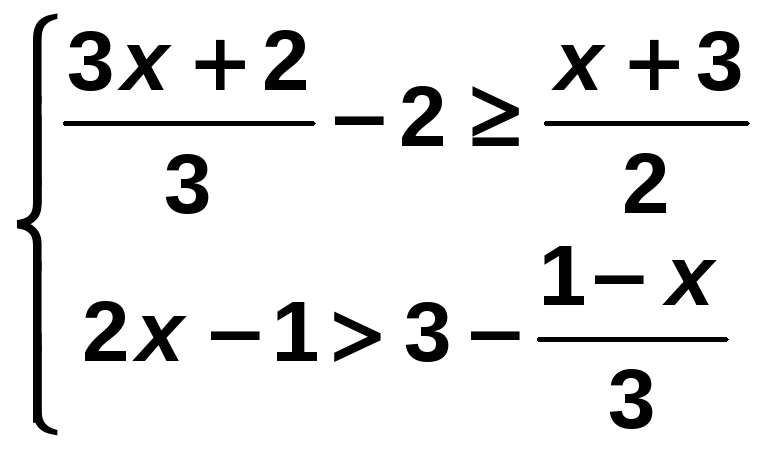
Solución:
Resolvemos cada inecuación y buscamos las soluciones comunes:
![]()
![]()
![]()

Ejercicio nº 11.-
Un fabricante de bombillas obtiene un beneficio de 0,80 € por cada pieza que sale de su taller para la venta pero sufre una pérdida de 1 € por cada pieza defectuosa que debe retirar.
En un día quiere fabricar 2 250 bombillas para obtener al menos un beneficio de 1 710 €. ¿Cuántas bombillas han de ser válidas?
Solución:
Llamamos:
x = “nº de bombillas válidas” → beneficio = 0,80x
2 250 − x = “nº de bombillas defectuosas” → pérdida = 1·(2 250 − x) = 2 250 − x
Se busca que el beneficio final sea mayor o igual que 1 710 € .
0,80x − 2 250 + x ≥ 1 710 → 1,80x ≥ 3 960 → x ≥ 2 200
Han de ser válidas por lo menos 2 200 bombillas.
Ejercicio nº 12.-
Escribe un sistema no lineal de dos ecuaciones con dos incógnitas que tenga como solución x = 3, y = −2. ¿Sería la única solución del sistema?
Solución:
Por ejemplo:
![]()
Otra solución de este sistema sería x = −2, y = 3.
Ejercicio nº 13.-
Resuelve el sistema:
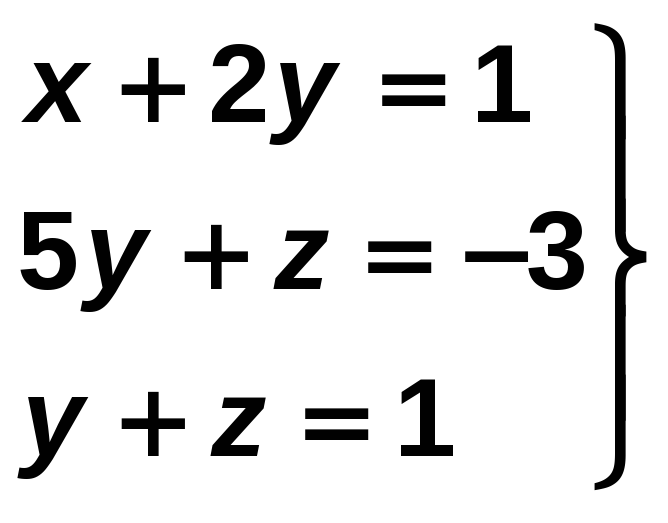
Solución:
Resolvemos el sistema formado por las dos últimas ecuaciones:
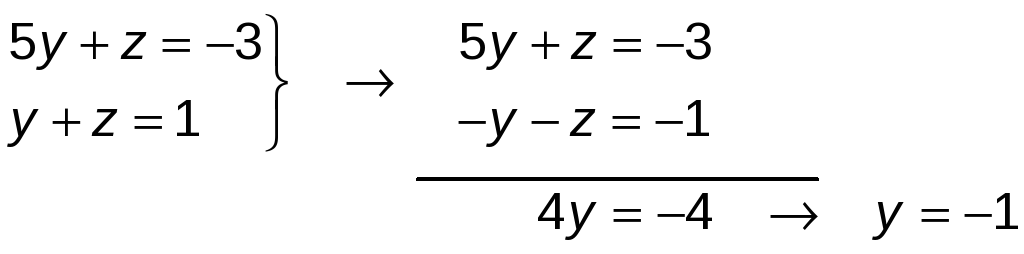
y + z = 1 → −1 + z = 1 → z = 2
Sustituyendo y = −1 en la primera ecuación, calculamos el valor de x:
x + 2 · (−1) = 1 → x − 2 = 1 → x = 3
La solución del sistema es x = 3, y = −1, z = 2.







