| Indice del artículo |
|---|
| ECUACIONES , INECUACIONES Y SISTEMAS. |
| Examen2 |
| EXAMEN 3 |
| EXAMEN 4 |
| EXAMEN 5 |
| EXAMEN 6 |
| Todas las páginas |
| Título de la materia: |
Matemáticas orientadas a las Enseñanzas Académicas |
||
| Nivel: | ESO 4 | Opción: | C |
| Nombre: | Grupo: | ||
| Evaluación: | N.º: | ||
| Calificación: | Fecha: |
Ejercicio nº 1.-
Resuelve las siguientes ecuaciones:
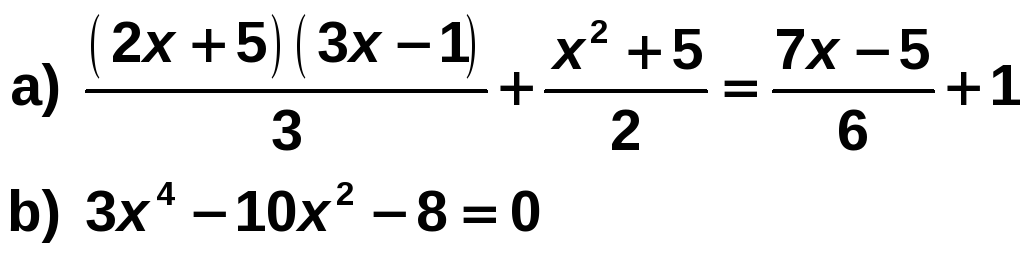
Solución:
a) Multiplicamos ambos miembros por 6:
![]()
![]()
![]()
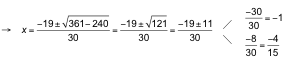
![]()
b) haciendo x2= z, se obtiene:
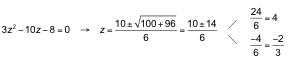
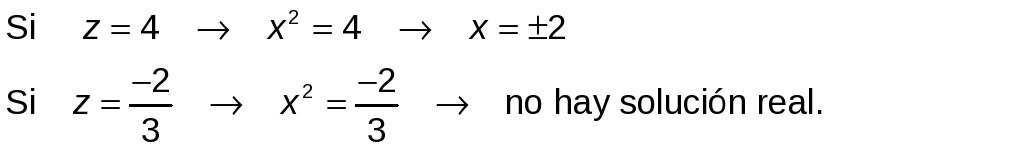
Las soluciones son x1= 2 y x2= −2.
Ejercicio nº 2.-
Resuelve:
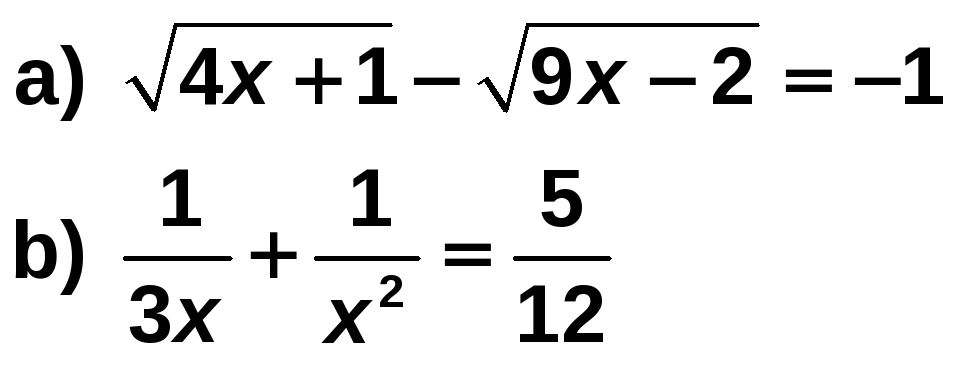
Solución:
![]()
Elevamos al cuadrado ambos miembros de la ecuación:
![]()
Volvemos a elevar al cuadrado:
![]()
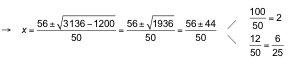
Comprobamos las dos posibles soluciones, sustituyendo en la ecuación inicial:
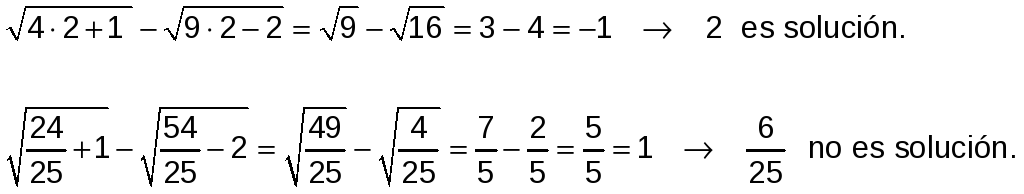
La única solución es x = 2.
b) Multiplicamos ambos miembros por 12x2, que es el mín.c.m. de los denominadores:
![]()
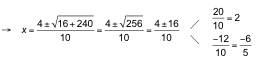
Comprobación:
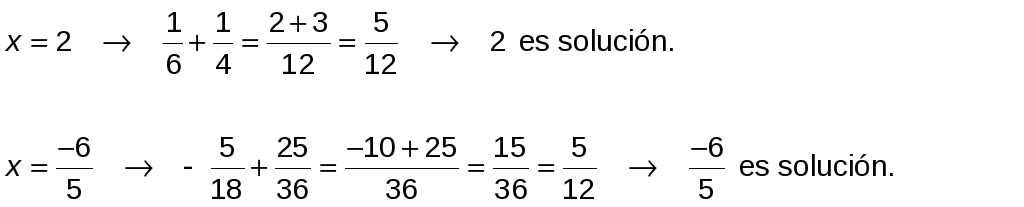
![]()
Ejercicio nº 3.-
![]()
Solución:
Consideramos cuatro polinomios de grado 1 cuyas ecuaciones tengan como raíces los valores
![]()
Se tiene, así:
![]()
![]()
Ejercicio nº 4.-
Resuelve las siguientes ecuaciones:
![]()
b) log2 (6x2 ‒ 2x) = 2
Solución:
![]()
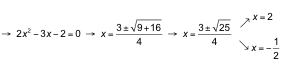
b) log2 (6x2 ‒ 2x) = 2 → 22= 6x2 ‒ 2x → 4 = 6x2 ‒ 2x →
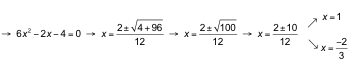
Las dos soluciones son válidas.
Ejercicio nº 5.-
![]()
en reformar la casa, el 10% de la cantidad inicial en ropa y el resto, 260 €, los ahorró. ¿Cuánto dinero heredó?
Solución:
x = "dinero heredado"

La ecuación que resuelve el problema será:
![]()
Multiplicamos ambos miembros por 30:
![]()
![]()
Ejercicio nº 6.-
Resuelve por el método que consideres más apropiado y comprueba la solución obtenida en el siguiente sistema:
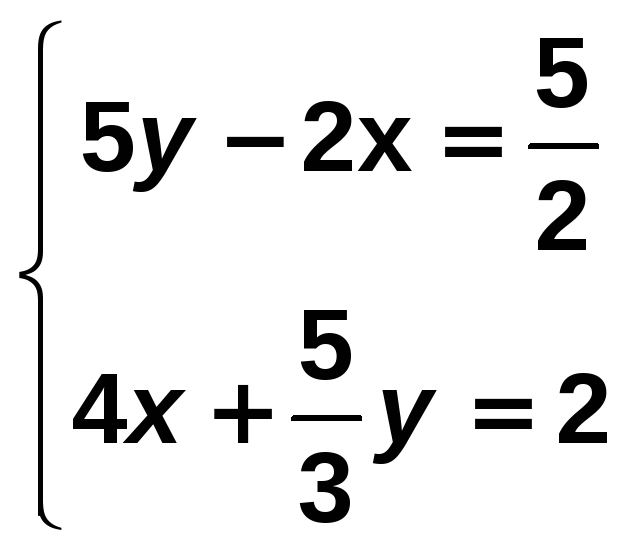
Solución:
Utilizamos el método de reducción en y ; para ello multiplicamos la 2ª ecuación por −3:
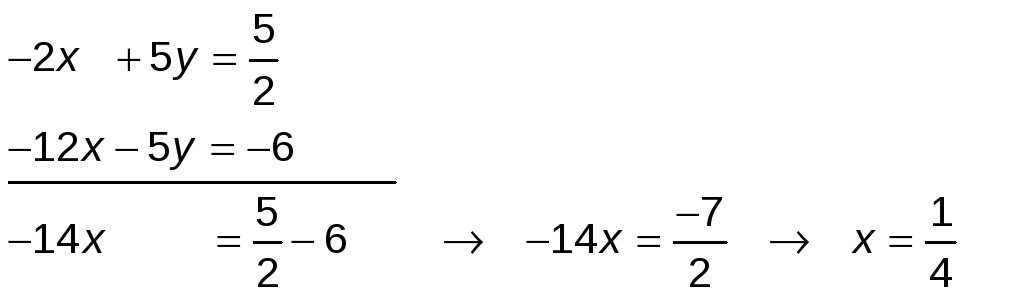
Calculamos y sustituimos el valor de x en la 1ª ecuación:
![]()
![]()
Comprobamos la solución:
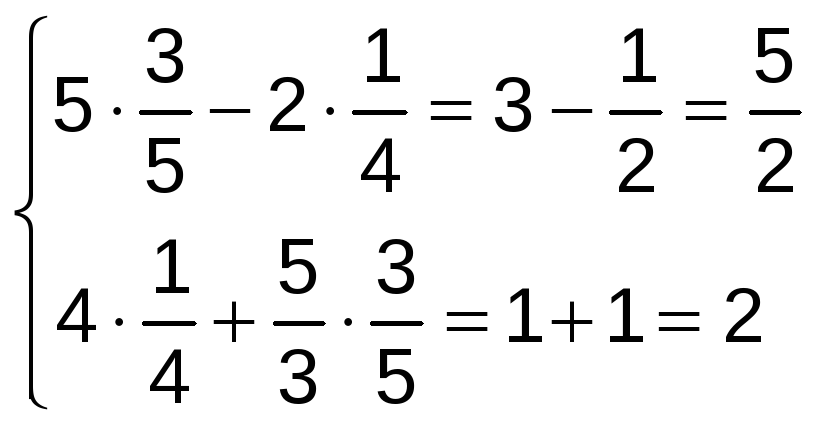
Ejercicio nº 7.-
Resuelve:
![]()
Solución:
![]()
Aplicamos el método de igualación:
![]()
Elevamos al cuadrado los dos miembros de la última igualdad:
![]()
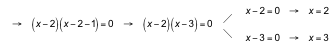
![]()
Comprobamos las soluciones sobre el sistema:
![]()
![]()
Ejercicio nº 8.-
Un bodeguero quiere mezclar vino de calidad superior cuyo precio es de 6 €/l con otro más corriente de 2 €/l. Dispone en total de 315 l. Calcula el número de litros de cada clase para que la mezcla cueste 4,4 €/l.
Solución:
x = “litros del vino que cuesta 6 €/ l ”
y = “litros del vino que cuesta 2 €/ l ”
El sistema a resolver será:
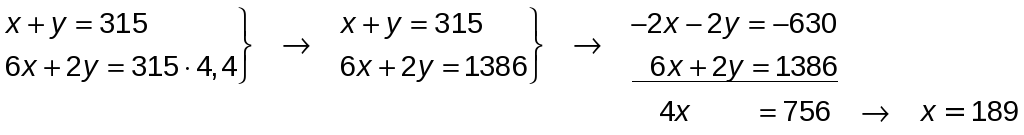
Luego, y = 315 − 189 = 126.
Ha de mezclar 189 l de vino bueno con 126 l del más corriente.
Ejercicio nº 9.-
a) Resuelve la siguiente inecuación y escribe la solución en forma de intervalo:
![]()
b) Resuelve la siguiente inecuación estudiando el signo de cada factor:
![]()
Solución:
![]()
La solución en forma de intervalo será: (−∞, −2)
b) El factor 5 − x = 0 si x = 5, y el factor x + 3 = 0, si x = −3.
Así:
![]()
Gráficamente:

Para que un producto de dos factores sea mayor que 0, ambos han de tener el mismo signo, luego la solución será el intervalo (−3, 5).
Ejercicio nº 10.-
Resuelve el siguiente sistema de inecuaciones:
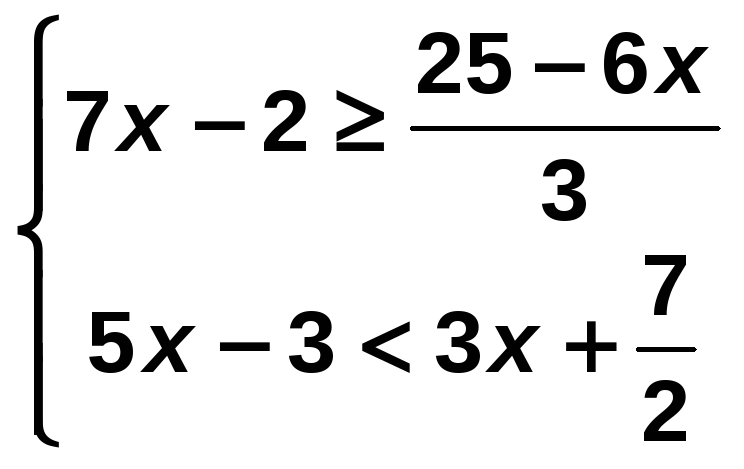
Solución:
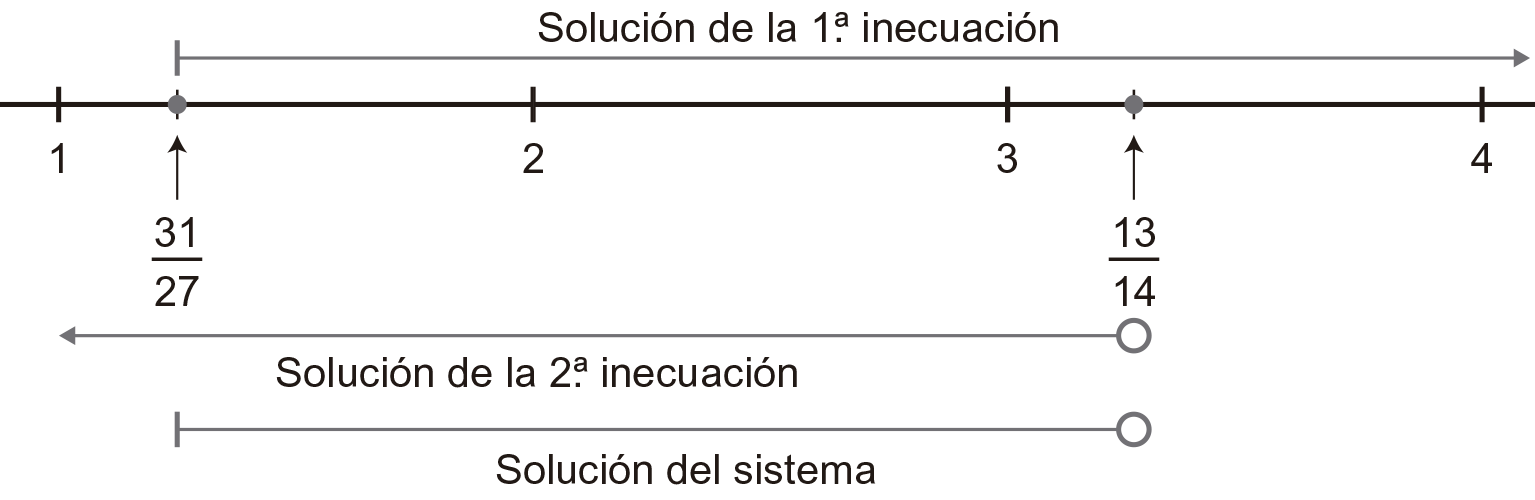
Resolvemos cada inecuación por separado y buscamos la solución que sea común a ambas:
![]()
![]()
![]()
Ejercicio nº 11.-
a) Un grupo de 6 personas han desayunado (café + bollería) pagando entre todos poco más de 10 €. ¿Qué puedes decir del precio de cada desayuno?
b) Al día siguiente, en ese mismo sitio, desayunaron 8 personas y les cuesta menos de 14 €. ¿Cuánto crees que costará el desayuno?
Solución:
![]()
El precio de cada desayuno supera los 1,66 €.

Uniendo ambos apartados deducimos que 1,66 x 1,75; luego es de suponer que el precio del desayuno será, más o menos, de 1,70 €.
Ejercicio nº 12.-
Calcula los valores que ha de tomar k para que la ecuación x2 − 6x + k = 0 tenga:
a) Dos soluciones iguales.
b) Dos soluciones que no sean números reales.
Solución:
a) Tendrá dos soluciones iguales cuando b2− 4ac = 0, es decir,
(−6)2− 4k = 0 → 36 − 4k = 0 → k = 9
b) Que las soluciones no sean números reales equivale a decir que la ecuación no tenga solución en el campo de los números reales; esto ocurre cuando b2− 4ac < 0.
36 − 4k < 0 → 36 < 4k → k > 9
Ejercicio nº 13.-
Resuelve:
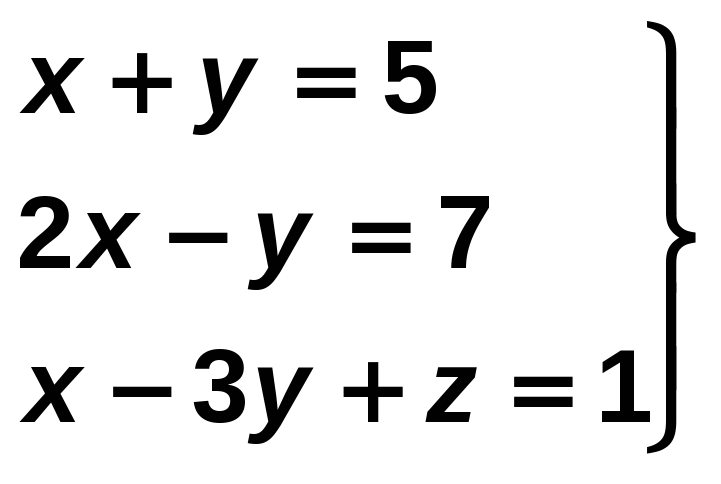
Solución:
Resolvemos el sistema formado por las dos primeras ecuaciones:
![]()
![]()
Sustituyendo x = 4, y = 1 en la tercera ecuación obtenemos z :
x − 3y + z = −1 → 4 − 3 · 1 + z = −1 → 4 − 3 + z = −1 → z = −2
La solución del sistema es x = 4, y = 1, z = −2.







