| Indice del artículo |
|---|
| Potencias. Resumen. |
| Propiedades |
| Ejercicios |
| Soluciones a los ejercicios |
| Distinta base |
| Raiz |
| juegos |
| Todas las páginas |
Operaciones con potencias de números con distinta base
Cuando trabajamos sólo con números y tenemos potencias de distinta base, debemos buscar que las potencias tengan la misma base, es decir hay que expresar todos las potencias con la misma base o si no es posible expresar todas las potencias con una sola base, con la mínima cantidad de bases posible.
¿Y cómo expresamos el número en otra base? Pues descomponiendo el número en factores.
Vamos a verlo con un ejemplo muy sencillo:
![]()
En esta multiplicación de potencias, en principio no podemos hacer nada, porque tenemos una multiplicación de potencias de distinta base y no podemos sumar sus exponentes.
Pero, el 4 lo podemos descomponer:
![]()
Por tanto, en la operación que estamos resolviendo, sustituimos el 4, por su descomposición y de esta forma nos ha quedado una multiplicación de potencias con la misma base:
![]()
Antes de multiplicar las potencias, hay que resolver el paréntesis, multiplicando los exponentes:
![]()
Ahora ya podemos multiplicar. Mantenemos la base y sumamos los exponentes
![]()
Al final, también podemos resolver la potencia.
Veamos otro ejemplo:
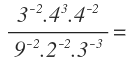
En principio, tenemos cuatro bases: 2, 3, 4 y 9.
Buscamos que todas las potencias tengan la misma base o el mínimo número de bases posible. Para ello, debemos descomponer en factores primos los números que se puedan y expresarlos de esta forma en la ecuación.
En este caso podemos descomponer el 4 y el 9, que los indicamos en la ecuación como 2² y 3²:

Nos han quedado dos bases: 2 y 3.
El siguiente paso es eliminar paréntesis, multiplicando los exponentes exteriores por los exponentes interiores:

En el numerador tenemos dos potencias con base 2 multiplicándose, por tanto, mantenemos la base y sumamos los exponentes. Hacemos lo mismo en el denominador con dos potencias de base 3:

Nos ha quedado una división de potencias de base 2 y otra de base 3. Para cada una mantenemos la base y restamos los exponentes:
![]()
Y con esto hemos terminado de simplificar la expresión, ya que no tenemos ningún exponente negativo.
Operaciones con potencias de distinta base elevada a otras potencias
Vamos a ver los pasos a seguir cuando tienes que simplificar una operación en la que tienes multiplicaciones y divisiones de distinta base, que además forman parte de otra potencia, como por ejemplo:

En primer lugar simplificamos todo lo posible en el interior del paréntesis.
Igual que antes, por un lado simplificamos los números y por otro lado, con cada base x e y, mantenemos las bases y restamos los exponentes:
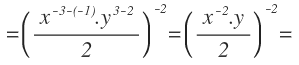
Ya no podemos operar más en el interior del paréntesis, por lo que procedemos a resolver el paréntesis.
Para resolver el paréntesis, hay que multiplicar el exponente de fuera, por cada uno de los exponentes que hay en el interior, según esta propiedad:
![]()
Al multiplicar exponentes nos queda:

Para terminar, tenemos que expresar la solución con todos los exponentes positivos.
Tenemos exponentes negativos en el numerador y en el denominador.
Te recuerdo que las potencias con exponente negativo que están en el numerador, pasan al denominador con exponente positivo y viceversa, según esta propiedad:

Aplicado a nuestra ecuación nos queda:

Terminamos la operación resolviendo la potencia de base 2.







