| Indice del artículo |
|---|
| ECUACIONES PRIMER Y SEGUNDO GRADO. |
| Segundo Grado |
| Incompletas b=0 |
| Ejercicios Online |
| MAS EJERCICIOS |
| Todas las páginas |
Veamos un video como introducción.
En general para resolver una ecuación de primer grado
debemos seguir los siguientes pasos:
1º Quitar paréntesis. Con la propiedad distributiva, ejemplo 2(x+3)=> 2x+6
2º Quitar denominadores. Con el m.c.m(denominadores)
3º Agrupar los términos en x en un miembroy los términos independientes en el otro. Con la transposición de términos: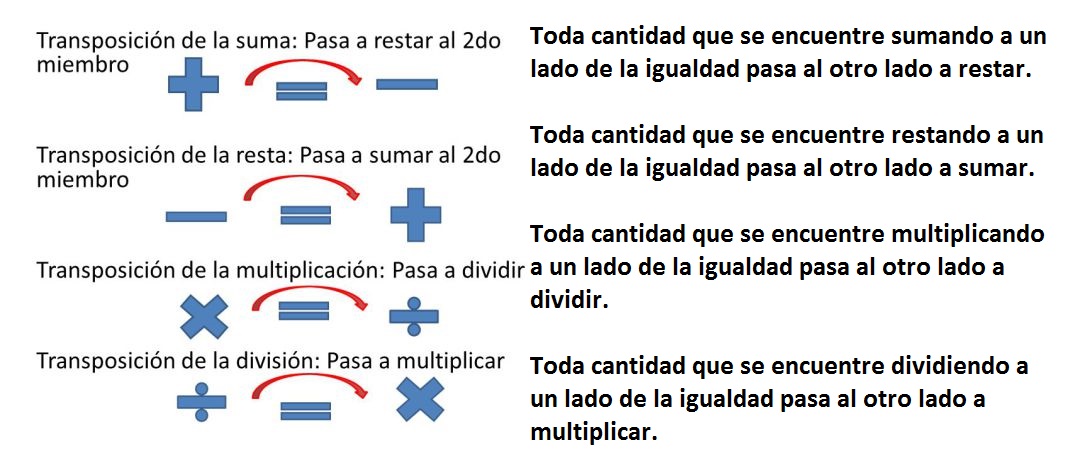
4º Reducir los términos semejantes.Suma de monomios
5º Despejar la incógnita.Dejar la x sola.
Calculo online paso por paso de una ecuaciónes.
Resolución de ecuaciones de segundo grado incompletas

Despejamos la incógnita:


Agrupamos los términos semejantes y los independientes, y sumamos:


Quitamos paréntesis:

Agrupamos términos y sumamos:

Despejamos la incógnita:


Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.


Quitamos paréntesis, agrupamos y sumamos los términos semejantes:

Despejamos la incógnita:


Quitamos paréntesis y simplificamos:

Quitamos denominadores, agrupamos y sumamos los términos semejantes:


Quitamos corchete:

Quitamos paréntesis:

Quitamos denominadores:

Quitamos paréntesis:

Agrupamos términos:

Sumamos:

Dividimos los dos miembros por: −9

Una ecuación de segundo grado es toda expresión de la forma:
ax² + bx +c = 0 con a ≠ 0.
Se resuelve mediante la siguiente fórmula:

1. 

2. 

3. 
Si es a < 0, multiplicamos los dos miembros por (−1).



Bingo de ecuaciones de 2º grado.
Una ecuación de segundo grado es toda expresión de la forma:
ax² + bx +c = 0 con a ≠ 0.
Se resuelve mediante la siguiente fórmula:

1. 

2. 

3. 
Si es a < 0, multiplicamos los dos miembros por (−1).


Una ecuación de segundo grado es incompleta cuando alguno de los coeficientes: b o c, o ambos, son iguales a cero, por tanto podemos encontrarnos con tres tipos de ecuaciones de segundo grado incompletas.
Primer caso si b = 0 y c = 0
ax² = 0
La solución es siempre x = 0.
ax² + c = 0 (Primer Tipo)
Las soluciones son: 
Veamos como se extraen las soluciones:
1. En primer lugar pasamos el término c al segundo miembro cambiado de signo.
2. Pasamos el coeficiente a al 2º miembro, dividiendo.
3. Se efecúa la ± raíz cuadrada porque si x² = 25 entonces:
Una solución es +5, ya que 5² = 25
La otra solución es (−5), ya que (−5)² = 25

Segundo caso si c = 0
ax² + bx = 0 (2º TIPO)
Las soluciones son: 
Veamos como se extraen las soluciones:
Extraemos factor común x:
x(ax + b) = 0
Como tenemos un producto igualado a cero o un factor es cero o el otro factor es cero o los dos son cero.
x = 0

Ejemplos
1. 
Sacamos factor común x

Como tenemos un producto igualado a cero un factor es cero o el otro factor es cero o los dos son cero
x = 0

2. 
Sacamos factor común 2x

Como tenemos un producto igualado a cero un factor es cero o el otro factor es cero o los dos son cero


Tercer caso si b = 0
Ejemplos
1. 
Pasamos el término independiente al segundo miembro

2. 
Pasamos el término independiente al segundo miembro y simplificamos dividiendo por 2

Por ser el radicando negativo no tiene solución en los números reales
SOLUCIONES
- 13
- a) x=0 y x=6
- b) x=0 y x=-27
- c) x=0 y x= -5 /3
- 14
- a)x=6 y x=-6
- b)
- c) No tiene solución.
- 15
- Click aquí para hacerlo Online
- 1. x2 -5x +6=0
B) x=-3, x=2
C) x=3, x=-2
D) x=3, x=2
- 2. x2 =-x+6
B) x=2, x=3
C) x=-2, x=-3
D) x=-2, x=3
- 3. x2 +2x=-1
B) x=1, x=1
C) x=-2, x=-1
D) x=-1, x=-1
- 4. x2 +x +1=0
B) x=2, x=2
C) No tiene solución en los R
D) x=-2, x=2
- 5. 2x2 -7x + 3=0
B) x=3, x=1/2
C) x=-3, x=1/2
D) x=-3, x=-1/2
- 6. x2 -5x = 84
B) x=12, x=7
C) x=12, x=-7
D) x=-12, x=-7
- 7. 2x2 + 3x = 27
B) x=3, x=-9/2
C) x=-3, x=-9/2
D) x=-3, x=9/2
- 8. 4x2 = -7x +2
B) x=-1/4, x=-2
C) x=-1/4, x=2
D) x=1/4, x=-2
- 9. 18 = 6x +x(x-13)
B) x=9, x=-2
C) x=9, x=2
D) x=-9, x=2
- 10. x2 + x/2 -1/2 = 0
B) x=-1/2, x=1
C) x=-1/2, x=-1
D) x=1/2, x=1
- 11. x2 -1=2(x+5) + 4
B) x=-5, x=3
C) x=5, x=-3
D) x=-5, x=-3
- 12. x2 + 5x/12 -1/6 =0
B) x=1/4, x=2/3
C) x=1/4, x=-2/3
D) x=-1/4, x=2/3
- 13. x2 -x + 1/4 =x/4
B) x=1, x=-1/4
C) x=-1, x=1/4
D) x=1, x=1/4
- 14. (x2 -1)/3 - (x-1)/6 = 2 + x/9
B) x=3, x=-13/6
C) x=3, x=13/6
D) x=-3, x=-13/6
- 15. 4x(x+1)=15
B) x=-3/2, x=-5/2
C) x=3/2, x=5/2
D) x=3/2, x=-5/2
- 16. x(x-2)=3
B) x=3, x=-1
C) x=3, x=1
D) x=-3, x=-1
- 17. -5x2 -15x+20=0
B) x=-4, x=1
C) x=4, x=1
D) x=4, x=-1
- 18. -3x2 +9x + 12 = 0
B) x=1, x=-4
C) x=-1, x=-4
D) x=-1, x=4
- 19. -2x2 + 10x -12 = 0
B) x=-2, x=3
C) x=-2, x=-3
D) x=2, x=3
- 20. x2 -4x +4=0
B) x=-2, x=-2
C) x=2, x=2
D) x=1/2, x=1/2
- 21. 18=6x +x(x-13)
B) x=-2, x=9
C) x=-2, x=-9
D) x=2, x=9

Ecuaciones cuadraticas por fórmula general







