| Indice del artículo |
|---|
| TEOREMA DE PITAGORAS |
| Aplicaciones |
| Problemas |
| Soluciones de los problemas |
| Inversa Pitagoras |
| Más problemas de aplicación |
| Ejercicios online con Thatquiz |
| Todas las páginas |
TEOREMA DE PITAGORAS
Video explicativo, por compañera.
En todo triángulo rectángulo se verifica que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
La lectura de este teorema se puede hacer desde dos sentidos:
- Si el triángulo es rectángulo se cumple la relación h2 = c12 + c22
- Si se cumple la relación anterior el triángulo es rectángulo.
Aplicaciones del Teorema de Pitágoras
El teorema de Pitágoras es de gran utilidad en multitud de problemas en los que se presenta algún triángulo rectángulo. Aquí puedes ver algunos
ejemplos.
-
Calcular la diagonal de un rectángulo.
-
Calcular la altura en algunos triángulos.
-
Calcular los lados de un rombo.
-
Calcular la altura de un trapecio
-
Calcular segmentos de tangente a una circunferencia.
-
Teorema de Pitágoras
En esta página resolvemos problemas aplicando el Teorema de Pitágoras. Este teorema establece que la suma de los cuadrados de los catetos de un triángulo rectángulo es igual al cuadrado de la hipotenusa:
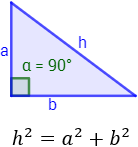
Recordad que un triángulo es rectángulo cuando uno de sus ángulos interiores es recto (90 grados) y que la hipotenusa es el lado opuesto al ángulo recto.
Problema 1
En el siguiente triángulo, ¿cuál de los lados es la hipotenusa y cuál es el ángulo recto?
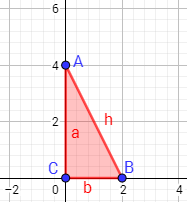
Calcular cuánto mide la hipotenusa.
Problema 2
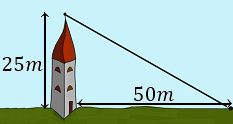
Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?
Problema 3
Una parcela de terreno cuadrado dispone de un camino de longitud 2√2 kilómetros (segmento discontinuo) que la atraviesa según se muestra en la siguiente imagen:
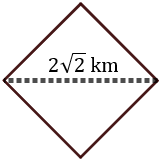
Calcular el área total de la parcela.
Problema 4
La hipotenusa de un triángulo rectángulo mide 10 metros y sus catetos miden x y x+2:
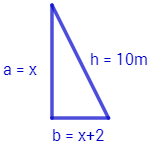
¿Cuánto miden los catetos?
Problema 5
Se desea pintar una cuadrado inscrito en una circunferencia de radio R=3cm como se muestra en la figura:
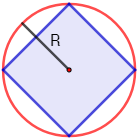
Calcular el área del cuadrado.
Problema 6
Calcular cuánto mide el cateto b de un triángulo rectángulo si su otro cateto, a, y su hipotenusa, h, miden
a=3√22 m
h=√1946 m
Problema 7
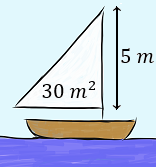
Hallar las medidas de los lados de una vela con forma de triángulo rectángulo si se quiere que tenga un área de 30 metros al cuadrado y que uno de sus catetos mida 5 metros para que se pueda colocar en el mástil.
Problema 8
Si el cateto de un triángulo rectángulo mide x y el otro mide el doble, obtener una fórmula para calcular la longitud de la hipotenusa en función del cateto menor, x.
Utilizar la fórmula obtenida para calcular la hipotenusa cuando x=√5 y x=2⋅√5.
Problema 9
Se tiene un rectángulo cuya base mide el doble que su altura y su área es 12 centímetros cuadrados. Calcular el perímetro del rectángulo y su diagonal.
Problema 10
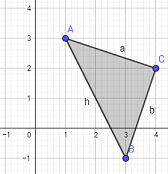
Calcular el área del triángulo rectángulo cuyos vértices son A=(1,3), B=(3,−1) y C=(4,2).
Problema 1
En el siguiente triángulo, ¿cuál de los lados es la hipotenusa y cuál es el ángulo recto?

Calcular cuánto mide la hipotenusa.
Los catetos son los lados a y b. La hipotenusa es el lado h. El ángulo recto es el ángulo que forman ambos catetos.
Para calcular la longitud de la hipotenusa, aplicamos Pitágoras. Los catetos miden a=2 y b=4, con lo que
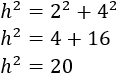
Finalmente, hacemos la raíz cuadrada:
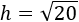
Simplificamos el resultado escribiendo el radicando como un producto y aplicando la propiedad de que la raíz de una producto es el producto de las raíces de sus factores:
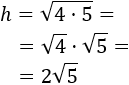
Si aproximamos, h≃4,47.
Problema 2

Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?
El cable coincide con la hipotenusa de un triángulo rectángulo cuyos catetos miden a=25m y b=50m.
Calculamos la longitud del cable (es la hipotenusa h):
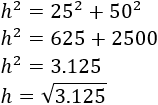
Como 3.125=252⋅5, podemos simplificar:
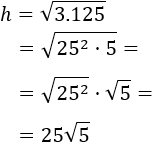
El cable debe medir h=25√5 metros, es decir, aproximadamente 55.9 metros.
Problema 3
Una parcela de terreno cuadrado dispone de un camino de longitud 2√2 kilómetros (segmento discontinuo) que la atraviesa según se muestra en la siguiente imagen:

Calcular el área total de la parcela.
Observando la figura, el camino coincide con una de las diagonales del cuadrado, así que divide a éste en dos triángulos iguales. Además, los dos triángulos son rectángulos y los catetos miden lo mismo.
Si llamamos x a la medida de los catetos, aplicando Pitágoras,
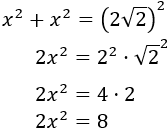
Hemos usado que el cuadrado de un producto es el producto de los cuadrados.
Para calcular x, pasamos el 2 dividiendo al otro lado de la igualdad y hacemos la raíz cuadrada:
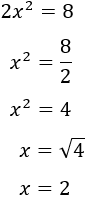
Por tanto, los cuatro lados de la parcela miden 2 kilómetros y, por consiguiente, su área es 4 kilómetros cuadrados.
Problema 4
La hipotenusa de un triángulo rectángulo mide 10 metros y sus catetos miden x y x+2:
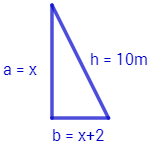
¿Cuánto miden los catetos?
Por Pitágoras, h2=a2+b2, con lo que
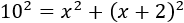
No olvidemos la fórmula del cuadrado de un binomio:
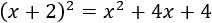
Sustituyendo,
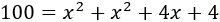
Simplificamos la ecuación:
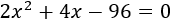
Resolvemos la ecuación de segundo grado:
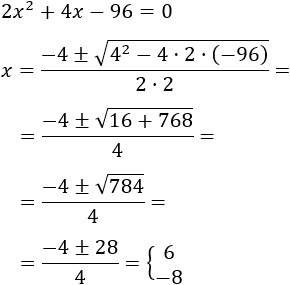
Como x representa una longitud, la solución debe ser positiva: x=6. Los catetos miden 6 y 8 metros.
Problema 5
Se desea pintar una cuadrado inscrito en una circunferencia de radio R=3cm como se muestra en la figura:

Calcular el área del cuadrado.
El radio mide R=3cm. El diámetro (d=2R) coincide con la diagonal del cuadrado y, por ende, divide al cuadrado en dos triángulos rectángulos iguales:
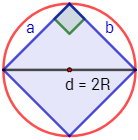
Como la figura es un cuadrado, los catetos a y b miden lo mismo, así que escribiremos simplemente a. La hipotenusa mide dos veces el radio: h=2⋅3=6cm.
Aplicamos el teorema de Pitágoras para calcular los lados del cuadrado:
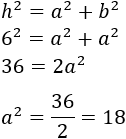
No calculamos la raíz cuadrada ya que no necesitamos saber cuánto miden los lados del cuadrado.
El área de un cuadrado de lado a es a2. Por tanto, el área del cuadrado inscrito es 18 centímetros cuadrados.
Problema 6
Calcular cuánto mide el cateto b de un triángulo rectángulo si su otro cateto, a, y su hipotenusa, h, miden
a=3√22 m
h=√1946 m
Por Pitágoras, sustituyendo a y h,
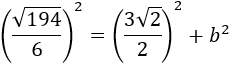
Aplicamos las propiedades de las potencias para calcular los cuadrados:
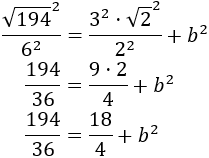
Calculamos b:
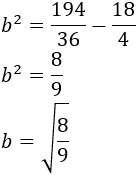
Aplicamos las propiedades de las raíces para simplificar:
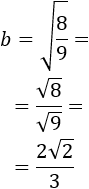
Por tanto, el cateto b mide 2√23 m.
Problema 7

Hallar las medidas de los lados de una vela con forma de triángulo rectángulo si se quiere que tenga un área de 30 metros al cuadrado y que uno de sus catetos mida 5 metros para que se pueda colocar en el mástil.
Llamamos a, b y h a la altura, base e hipotenusa de la vela.
Por un lado, como el área de un triángulo es base por altura, tenemos
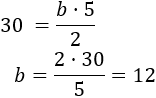
De donde tenemos que la base debe medir 12 metros.
Por otro lado, como la vela tiene forma de triángulo rectángulo, podemos calcular la hipotenusa por Pitágoras:
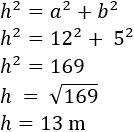
Por tanto, los lados de la vela deben medir 5, 12 y 13 metros.
Problema 8
Si el cateto de un triángulo rectángulo mide x y el otro mide el doble, obtener una fórmula para calcular la longitud de la hipotenusa en función del cateto menor, x.
Utilizar la fórmula obtenida para calcular la hipotenusa cuando x=√5 y x=2⋅√5.
Supongamos que uno de los catetos mide x, entonces el otro debe medir 2x. Para calcular la hipotenusa, h, aplicamos Pitágoras:
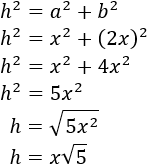
Aplicamos la fórmula para x=√5:
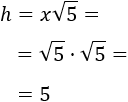
Aplicamos la fórmula para x=2⋅√5:
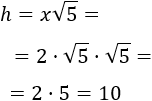
Problema 9
Se tiene un rectángulo cuya base mide el doble que su altura y su área es 12 centímetros cuadrados. Calcular el perímetro del rectángulo y su diagonal.
Llamamos a y b a la altura y la base del rectángulo, respectivamente. Como la base es el doble que la altura, b=2a.
El área de un rectángulo es base por altura, así que
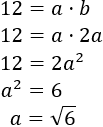
La altura del rectángulo mide √6cm y la base mide 2√6cm. El perímetro del rectángulo es 6√6cm.
Como la diagonal del rectángulo lo divide en dos triángulos rectángulos y sabemos cuánto miden los catetos, aplicamos Pitágoras para calcular la diagonal, d:
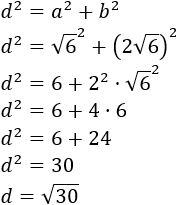
La diagonal del rectángulo mide √30 centímetros.
Problema 10

Calcular el área del triángulo rectángulo cuyos vértices son A=(1,3), B=(3,−1) y C=(4,2).
Observad la siguiente figura:
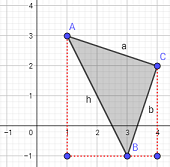
Podemos calcular el lado h y el lado b aplicando dos veces Pitágoras ayudándonos de los segmentos de color rojo, que forman triángulos rectángulos.
Los catetos del triángulo cuya hipotenusa es h miden 2 y 4 unidades. Por tanto,
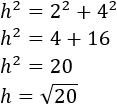
Los catetos del triángulo cuya hipotenusa es b miden 1 y 3 unidades. Por tanto,
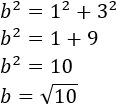
Conocemos la hipotenusa, h, y la base, b, del triángulo del problema. Aplicamos Pitágoras para calcular la altura a:
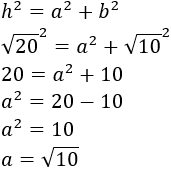
Calculamos el área del triángulo (base por altura entre 2):
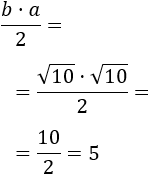
El área del triángulo es 5 unidades al cuadrado.
1. Introducción
Teorema: dado un triángulo rectángulo de catetos a y b e hipotenusa h (el lado opuesto al ángulo recto). Entonces,
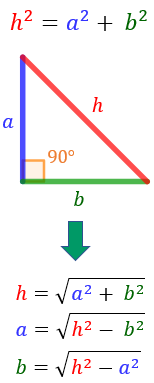
Recordemos que:
-
el triángulo es rectángulo porque tiene un ángulo recto, es decir, un ángulo de 90 grados ó π / 2 radianes.
-
la hipotenusa es el lado opuesto al ángulo recto
Nota: h siempre es mayor que los dos catetos, es decir, h > a y h > b.
El teorema de Pitágoras es uno de los resultados más conocidos de las matemáticas y también uno de los más antiguos. Existen cientos de demostraciones de este resultado.
La pirámide de Kefrén (siglo XXVI a. C.) fue construida en base al llamado triángulo sagrado egipcio, que es el triángulo rectángulo de lados 3, 4 y 5.
La comprensión del teorema es sencilla y tiene muchas aplicaciones en la vida cotidiana, como veremos en los problemas de esta sección. Pero también tiene sus aplicaciones en las matemáticas avanzadas (análisis vectorial, análisis funcional...).
2. 12 Problemas Resueltos
Problema 1
Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.
Problema 2
Si la hipotenusa de un triángulo rectángulo mide 2cm y uno de sus lados mide 1cm, ¿cuánto mide el otro lado?
Problema 3
Calcular la hipotenusa del triángulo rectángulo cuyos lados miden 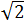 y
y 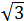 .
.
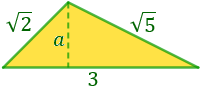
Problema 4 (dificultad muy alta)
Calcular la altura del siguiente triángulo sabiendo que sus lados miden 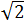 ,
, 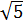 y su base 3.
y su base 3.
Problema 5
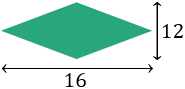
Calcular el perímetro del siguiente rombo si sabemos que sus diagonales (altura y anchura) miden 16 y 12.
Problema 6
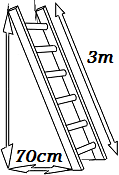
Calcular la altura que podemos alcanzar con una escalera de 3 metros apoyada sobre la pared si la parte inferior la situamos a 70 centímetros de ésta.
Problema 7
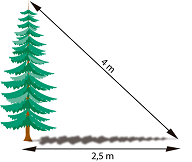
Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
Problema 8
La medida que se utiliza en los televisores es la longitud de la diagonal de la pantalla en unidades de pulgadas. Una pulgada equivale a 2,54 centímetros:
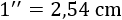
Si David desea comprar un televisor para colocarlo en un hueco de 96x79cm, ¿de cuántas pulgadas debe ser el televisor?
Problema 9
Un clavadista está entrenando en una piscina con una plataforma. Cuando realiza el salto, cae a una distancia de 1 metro de la plataforma sumergiéndose 2,4 metros bajo el agua. Para salir a la superficie, bucea hasta el final de la piscina siguiendo una línea transversal de 8,8 metros de longitud.
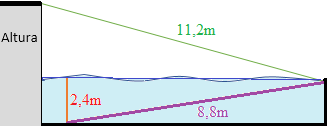
Si la longitud desde la parte superior de la plataforma al lugar en donde emerge del agua es de 11,2 metros, ¿cuál es la altura de la plataforma (desde el nivel del agua)?
Problema 10
Un aparcamiento con forma rectangular de dimensiones 35x98 metros es controlado por cuatro cámaras de vigilancia.
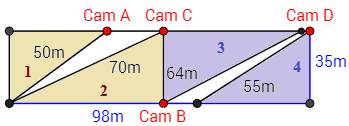
La cámara A observa el área 1; la cámara B, el área 2; la cámara C, el área 3; y la cámara D, el área 4.
Calcular el porcentaje del área del aparcamiento que no es vigilada por ninguna cámara.
Problema 11
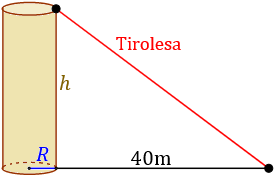
Un parque de diversiones quiere construir una nueva atracción que consiste en una tirolesa que parte desde la base superior de una columna con forma cilíndrica. Si el radio de la columna es R=2m
metros y el área de su lateral es de 120 metros cuadrados, calcular la longitud del cable de la tirolesa para que alcance el suelo a 40 metros de distancia de la columna.
Problema 12 (dificultad alta)
Distancias Sol-Tierra-Luna. Supongamos que la luna está en la fase de su primer cuarto, lo que significa que desde la Tierra la vemos del siguiente modo

siendo la mitad clara la que vemos, es decir, la iluminada por el Sol.
Sabemos que la distancia de la Tierra a la Luna es de 384100km y de la Tierra al Sol es de unos 150 millones de kilómetros. Se desea calcular la distancia de la Luna al Sol en esta fase (considerar las distancias desde los centros).
Plantear el problema, pero no es necesario calcular el resultado.
Más problemas: Problemas de Pitágoras (PyE).







