| Indice del artículo |
|---|
| Articulos recomendables para leer. |
| TCordobes |
| Noticia Periodico erronea |
| Iteraciones Sucesiones |
| Todas las páginas |
En busca de simetría
- 4 junio, 2019
- Matemáticas para pensar
- 2 MIN
Un palíndromo es una palabra, una expresión o un número que se lee igual de izquierda a derecha, que de derecha a izquierda. En el caso de los números se utiliza también la expresión “números capicúas”. Contrariamente a lo que ocurre con las palabras o expresiones, es fácil obtener números palíndromos, de hecho, existen infinitos. Basta con tomar un número finito de cifras y repetirlas en sentido inverso, repitiendo, o no, el término del medio: 232, 3.773, 57.675, etcétera.
Tomemos un número cualquiera de dos dígitos, por ejemplo, el 23, que claramente no es igual a su simétrico, el número, 32, luego no es capicúa. ¿Qué ocurrirá si sumamos ambos, el número inicial y su simétrico? Veámoslo, 23 + 32 = 55. Obtenemos un número capicúa. ¿Ocurrirá esto con más números? Consideremos otro número, por ejemplo, el 57 y sumémosle su simétrico, 57 + 75 = 132, que, sin embargo, no es capicúa. Pero, probemos a realizar el mismo proceso de sumarle su simétrico al resultado anterior: 132 + 231 = 666, que resulta sí ser capicúa. Sigamos probando. El número 68, le sumamos su simétrico, 68 + 86 = 154, continuamos el proceso, 154 + 451 = 605, y un paso más, 605 + 506 = 1111, hasta que, de nuevo, obtenemos un número capicúa. Aunque esta vez hemos necesitado 3 pasos, o iteraciones. Podemos plantearnos, por lo tanto, el siguiente problema:
¿Si tomamos cualquier número natural y le sometemos al proceso iterativo de “sumar el simétrico del número”, se alcanzará siempre un número capicúa, es decir, tras un un número finito de pasos se obtendrá un palíndromo?
Empecemos viendo qué ocurre con los números de dos dígitos:
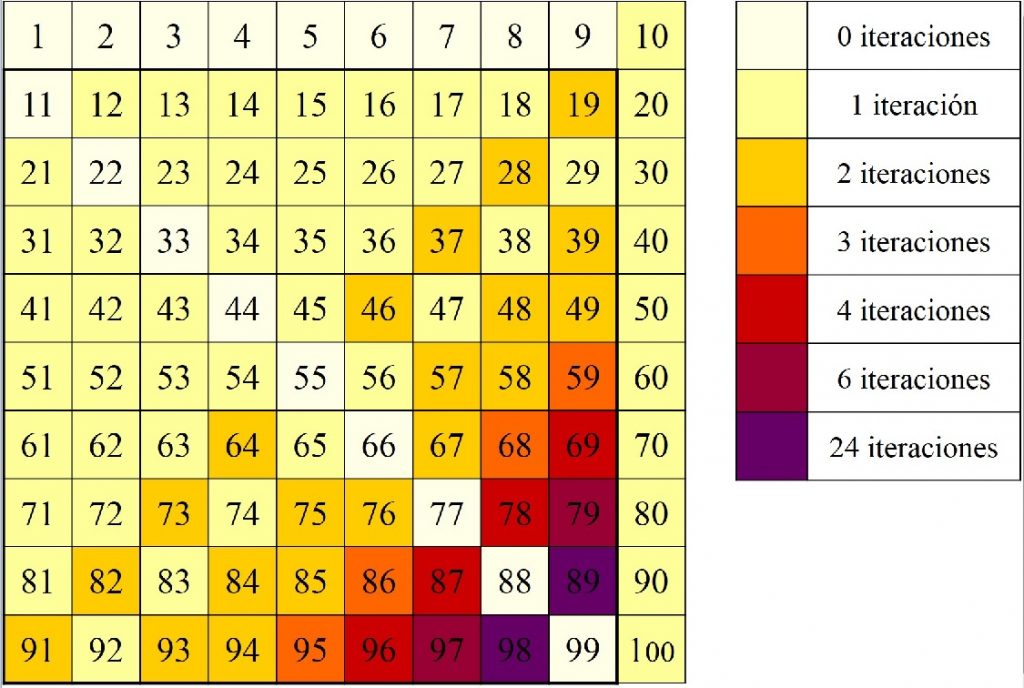
Para estos la respuesta es afirmativa, aunque para el 89, y su simétrico 98, se han necesitado 24 iteraciones para llegar al palíndromo. ¿Seguirá siendo cierta esta propiedad para números más grandes de tres o más dígitos? Lo cierto es que, a día de hoy, no se sabe la respuesta a esta pregunta. Este sigue siendo un problema matemático abierto. De hecho, el número 196, que no es muy grande, se desconoce si genera, mediante este proceso, un número capicúa.
La sucesión de los resultados de las 20 primeras iteraciones del número 196 es: 196, 887, 1.675, 7.436, 13.783, 52.514, 94.039, 187.088, 1.067.869, 10.755.470, 18.211.171, 35.322.452, 60.744.805, 111.589.511, 227.574.622, 454.050.344, 897.100.798, 1.794.102.596, 8.746.117.567, 16.403.234.045 y 70.446.464.506, que claramente no son palíndromos.
En la década de los años 80 se utilizaron los ordenadores para generar esta sucesión de números y averiguar si termina, o no, en un número capicúa. En 2011, Romain Dolbeau, con su programa “p196_mpi”, consiguió realizar un billón de iteraciones, con las cuales alcanzó un número de más de 400 millones de dígitos, sin conseguir el deseado capicúa. Y en 2015 alcanzó un número con un billón de dígitos, aún sin conseguir el objetivo de llegar a un palíndromo.
De hecho, el 196 no es el único número del que se desconoce si termina, con el proceso de “sumar el simétrico”, en un palíndromo. A la sucesión de números sospechosos de no generar un número capicúa se la conoce como sucesión de números Lychrel y es la sucesión A023108 en la Enciclopedia on-line de sucesiones de números enteros, de N. J. A. Sloane. Los primeros términos de esta sucesión son:
196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986, 1.495, 1.497, 1.585, 1.587, 1.675, 1.677, 1.765, 1.767, 1.855, 1.857, 1.945, 1.947, 1.997, …







