―Ya, ya, lo tengo.

―¿Sí? ¡Dime, dime!

―Y tus besos nos gustan más que comer tortellinis -respondió Ven.
―No se dice tortellinis, ya te lo he explicado, tortellini es plural.
―Ah, es verdad, mejor, sin ‘s’ queda mejor.
―Pero tortellini ya lo usamos el año pasado- se quejó un poco abatido Sal, mientras subía sus gafotas arrugando la nariz.
―Jo, es verdad… ¿Le hacemos un dibujo con flores? ¿Con muchas flores? Le encantan las flores.

Gauss miraba atentamente con sus ojitos marrones a sus dos amiguitos, pareciera que tratara de ayudarlos en su empeño. Sal alargó su mano y le acarició el lomo.

―Pero ¿qué les pasa a estos chicos?
―Hola, Mati ―dijo Sal sin levantar la vista de Gauss.
―Hola, Mati ―dijo Ven―. No nos sale el poema de la abuela.
―¿Estáis haciendo un poema?
―Sí ―siguió contando el pequeño―, esta tarde vamos al cumple de la abuela y queríamos hacerle un poema, como el año pasado…
―Le gustó tanto ―continuó Sal― que hasta lloró de la alegría.
―No me extraña, sois dos nietos muy lindos ¿Y qué os pasa este año?
―Que no encontramos nada que rime con Trini ―se quejó Sal.
―Bueno, sí, tortellinis, tortellini ―rectificó hábilmente Ven―, pero ya lo usamos el año pasado.

―Dejadme pensar… ―dijo la pelirroja con aire teatral―… Ya está, ya lo tengo.
―¿El qué? ―dijeron al unísono Sal y Ven.
―Os enseñaré un truco de magia y esta tarde, en la merienda, le hacéis una actuación de magia a vuestra abuela Trini como regalo de cumpleaños.
―¡Mola, mola! ―gritaron los dos.
―¿Cuántos años cumple la abuela?
―60 ―respondieron al unísono.
―Muy bien ―continuó ella―. Pensad un número del 1 al 60, entre vosotros, pero no me lo digáis.

Sal y Ven se abrazaron por el cuello, ocultando sus caritas de Mati y cuchichearon hasta acordar cuál sería el número elegido. Eligieron el 42 por ser el número de su casa.

―Ya ―dijeron.

Mati entonces les dio estas seis tarjetas repletas de números:

―Tomad. Revisad en cuáles de estas tarjetas está vuestro número y las colocáis hacia arriba. Poned boca abajo las tarjetas que no tengan vuestro número.

Los dos niños revisaron con curiosidad cada tarjeta, mirando de cuando en cuando a Mati por el rabillo del ojo, para asegurarse de que no estaba haciendo trampas. Al final de la revisión, habían dejado boca arriba estas tarjetas:

-Dejadme pensar un rato… que vosotros sois dos y muy listos… -Mati creaba expectación mientras miraba las tres tarjetas.

―¿Podría ser el…42? –dijo al cabo de unos segundos

Los dos pequeños se quedaron sin palabras, Gauss ladró (aún no se sabe muy bien por qué, igual pasó una mosca en ese preciso instante)

―Mati, ¡eres mágica de verdad! ―balbuceó Sal.
―¿Nos puedes conseguir un autógrafo de Messi? ―Ven estaba hasta pálido.
―Bueno, bueno, no es exactamente magia, son matemáticas, la Magia del 2, os contaré el truco y no, me temo que no tengo el poder de conseguir lo de Messi.

Mati puso las tres tarjetas elegidas por ellos en la mesa y fue señalando una a una.

―Fijaos en las cuatro esquinas de esta tarjeta ―les pidió.

―¿Cuál es el más pequeño de los cuatro números de las esquinas? ―les preguntó.
―El 2 ―contestaron.
―¿Y en esta otra?

―El 8 es el más pequeño ―dijo Ven, con cierto aire ufano.
―Muy bien, el 8, que es 2×2×2, ó 2³ que se dice, 2 elevado a 3 ―continuó Mati―, ya tenemos 2 y 8 que suman 10. ¿Y en la última de las tres? ¿Cuál es el número más pequeño de las esquinas?

―El 32 ―dijeron ambos.
―32 que es 2×2×2×2×2, ó 2⁵ que se dice, 2 elevado a 5. Teníamos 10 más 32, ya está 42, el número que habíais pensado los 2.
―¡Toma! ¡Cómo mola, Mati! ―Ven seguía alucinando con el truco y Sal seguía aún un poco reticente.

―Otra vez, Mati, por favor ―pidió nuestro gafotas.
―¿Lo has pensado ya?
―Sí.
―Elige las tarjetas que lo tienen.

Después de la revisión, Sal dijo que no estaba en ninguna.

―Eso no puede ser, cariño. ¿Qué número pensaste?
―El 100, para ver si funciona siempre o sólo con los años de la abuela.
―No, para poder elegir números hasta el 100 necesitamos 1 tarjeta más.
―Jo, no entiendo nada, Mati ―se quejó Sal.
―Con estas tarjetas sólo podemos hacerlo hasta 63. Hemos hecho las tarjetas del 1, 2, 4, 8, 16 y 32, (es decir, del 2⁰, 2¹, 2², 2³, 2⁴ y 2⁵ ), que sumadas todas llegan hasta el 63. Para hacer número mayores que 63, necesitaríamos la tarjeta del 64 (2⁶) donde pondríamos los números correspondientes entre 64 y 127.
―Mati, es un lío… ¿Cuáles son los números correspondientes? ―suplicó nuestro gafotas.

Mati sacó su pizarra y les anunció que les iba a explicar las matemáticas que había dentro de esta magia.

―¿Nos lo cuentas, porfi?
―Mirad, elegid un número cualquiera.
―Ya ―dijo Ven.
―¿Cuál es? ―preguntó la pelirroja.
―Ja, no te lo diré, adivínalo ―dijo muy digno Ven.
―Pero si es para explicarte en qué tarjetas está y por qué.
―Ah, entonces, vale, el 43.
―Vamos a dividir por 2, ¿cuánto nos da?
―21, pero sobra 1 ―respondió rápido Sal.
―Volvemos a dividir por 2 ―pidió Mati.
―10 y sobra 1 ―dijo Sal.
―Dividimos de nuevo y…
―5 y te sobra 0 ―dijo Ven, orgulloso
―Seguimos dividiendo por 2 …
―2 y sobra 1.
―Y dividimos por 2 y tenemos…
―1 y sobra 0 ―respondieron los 2.

Mati había estado escribiendo en su pizarra y tenía esto:

―Ahora ―les dijo― nos fijaremos en el último resultado, 1, y en lo que nos ha ido sobrando, los restos, fijaos…

―Y ―siguió explicando Mati― los escribimos de abajo a arriba, así 43 será representado por 101011. Ahora fijaos, lo ponemos en esta tabla:

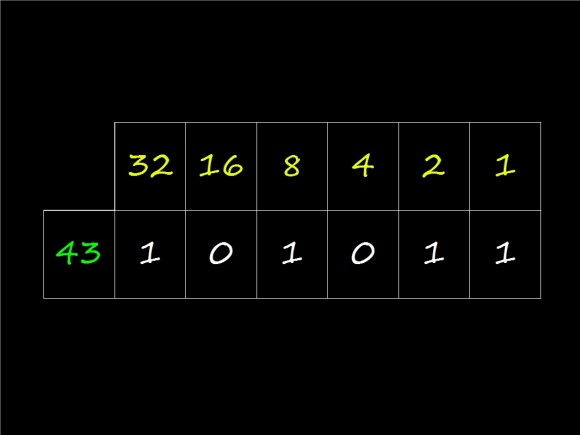
Mati continuó diciendo:

―Eso significa que 43 aparecerá en las tarjetas que tengan un 1 en su correspondiente casilla, es decir, el 43 estará en la tarjeta del 32, del 8, del 2 y del 1, que suman, exactamente 43.

―¡Yo quiero hacerlo!¡Por favor, Mati, por favor! ―dijo Sal, arrugando su naricilla como hacía con mamá para convencerla―. ¡Con el 25!

Mati le cedió la tiza y él escribió:

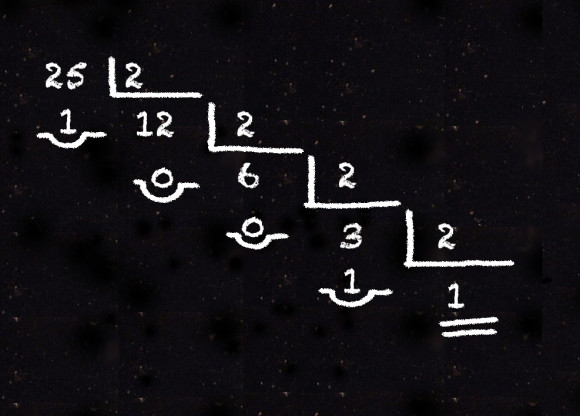
―Así que 25 será… ―pensaba Sal― 11001.

Sal se dispuso a ponerlo en una tabla como Mati pero bufó:

―Lo sabía, Mati, no funciona ¡Sólo tengo 5 números y son 6 tarjetas!

―Ah, se me olvidó contaros, si salen menos de 6, le ponéis tantos ceros delante como sean necesarios.
―Entonces el 25 es ¿011001?
―Muy bien, Sal, ¿en qué tarjetas estará?

El niño hizo su tabla:

―En la del 16, la del 8 y la del 1, ¡cómo mola! ¡16+8+1 es 25!

―Ey, yo quiero ―pidió Ven

―Venga, le animó Mati

Le dio su tiza y Ven escribió:

―Así que 13 sale 1101… ―mascullaba Ven―. Le pongo 2 ceros delante para tener 6 números… ¡001101! Hago la tabla

Con una sonrisa de oreja a oreja, Ven hizo su tabla:

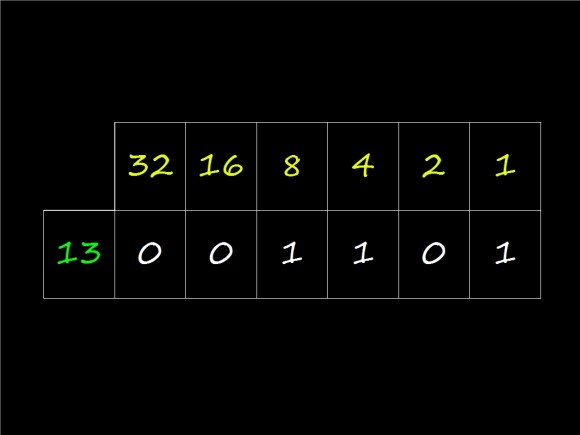
―¡¡Toma, toma, toma!! En la del 8, la del 4 y la del 1, 8+4+1 es ¡13!

Mati disfrutaba viéndolos sonreír y haciendo cuentas y tablas en la pizarra, les dio un beso suave en el pelo a cada uno y desapareció sin que nadie, excepto Gauss, se diera cuenta. Ya volvería en otro momento a recoger su utillaje.

Aquella tarde, el espectáculo de los dos hermanos en casa de los abuelos comenzaba con ellos, muy artistas, diciendo al unísono:

“Feliz cumpleaños,
querida abuela Trini.
Hoy te regalamos la magia
de los hermanos Houdini.”.

FIN

Pues bien. La escritura que hemos hecho de 43, 25 y 13 usando 0 y 1, no sólo es útil para hacer trucos de magia.

Se trata del Sistema Binario de numeración en el que todos los números se representan utilizando sólo 0 y 1, y que se usa mucho en Informática, entre otras muchas cosas, para programar los juegos que tanto nos gustan de la DS, la Wii, la Xbox, etc…

Te propongo un reto:

Trata de encontrar en la siguiente tabla las expresiones binarias de los números del 1 al 10. Éstos se pueden encontrar de arriba abajo, de abajo a arriba, de izquierda a derecha o de derecha a izquierda.

Para ello primero debes escribir del 1 al 10 en binario, por ejemplo, para escribir 9, vamos dividiendo 9 entre 2, hasta llegar a 1, y luego nos quedamos con el 1 final y todos los restos obtenidos, de abajo hacia arriba:

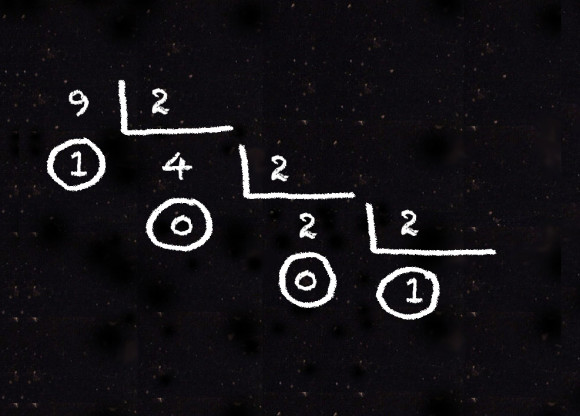
Por lo tanto, 9= 1 0 0 1

Una vez tengas escrito los números del 1 al 10 en binario, puedes empezar la sopa.

Si te quedas con más ganas de “sopa”, en ésta puedes encontrar hasta el 30.

Y ahora ya puedes entender este chiste:

“Sólo hay 10 tipos de personas en el mundo: los que saben binario y los que no”

Hasta pronto.

MATI

P.S: Si haces tus tarjetas y no te sale el truco, una de dos: o sumaste mal las esquinas más pequeñas o bien tu compañero no revisó bien en todas las tarjetas. Te dejemos aquí las 6 tarjetas en tamaño grande por si las quieres imprimir (pincha sobre ellas y se ampliarán)