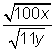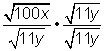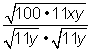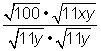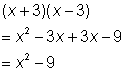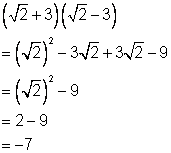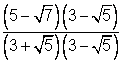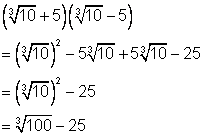TROTAMATES

Racionalizando denominadores

Objetivos de aprendizaje

· Racionalizar un denominador con un monomio que contiene una raíz cuadrada.

· Racionalizar un denominador que contiene dos términos.

Si bien los radicales siguen las mismas reglas que los enteros, a veces es difícil encontrar el valor de una expresión que contiene radicales. Por ejemplo, probablemente tienes una idea de cuánto es  y  , pero ¿y las cantidades  y ? Estas son más difíciles de visualizar.

Dicho esto, algunas veces tendrás que trabajar con expresiones que contienen muchos radicales. Normalmente el valor de estas expresiones no es claro a simple vista. En casos donde tienes una fracción con un radical en el denominador, puedes usar una técnica llamada racionalizando un denominador para eliminar el radical. El objetivo de racionalizar un denominador es que sea más fácil de entender cuál es el valor de la cantidad al eliminar los radicales de los denominadores.

La idea de racionalizar un denominador tiene sentido si consideras la definición de “racionalizar.” Recuerda que los números 5, , y  son todos números racionales, cada uno puede expresarse como la razón de dos enteros (, y  respectivamente). Algunos radicales son números irracionales porque no pueden representarse como la razón de dos enteros. Como resultado, el objetivo de racionalizar un denominador es cambiar la expresión de tal forma que el denominador se vuelve un número racional.

Aquí hay algunos ejemplos de denominadores racionales e irracionales.

Ahora examinemos cómo pasar de un denominador irracional a uno racional.

Empecemos con la fracción . Su denominador es , un número irracional. Esto hace difícil imaginar el valor de .

Puedes renombrar esta fracción sin cambiar su valor, si multiplicas por 1. En este caso, 1 igual a . Observa lo que pasa.

El denominador de la nueva fracción ya no es un radical (observa, sin embargo, que el numerador sí lo es).

Entonces, ¿por qué multiplicar  por ? Sabías que la raíz cuadrada de un número por sí misma será un número entero. En términos algebraicos, esta idea está representada por . Observa de nuevo los denominadores en la multiplicación de . ¿Ves dónde ?

Aquí hay otros ejemplos. Observa cómo el valor de la fracción no cambia, simplemente se multiplica por un equivalente de 1.

Puedes usar el mismo método de racionalizar denominadores para simplificar fracciones con radicales que contienen una variable. Siempre y cuando multipliques la expresión original por un equivalente de 1, puedes eliminar un radical en el denominador sin cambiar el valor de la expresión.

Racionalizar el denominador y simplificar.  A)  B)  C)  D)

Los denominadores no siempre contienen sólo un término, como se ha visto en los ejemplos anteriores. Algunas veces, encontrarás expresiones como  donde el denominador está compuesto de dos términos,  y +3.

Desafortunadamente, no puedes racionalizar estos denominadores de la misma manera que haces con denominadores de un término. Si multiplicas  por , obtienes . El  original desaparece, pero ahora aparece la cantidad  ...¡Esto no es una mejora!

Para racionalizar este denominador, quieres elevar al cuadrado el término radical y de alguna forma evitar que el término entero se multiplique por el radical. ¿Es esto posible?

Sí es posible y ya has visto cómo se hace!

Recuerda que cuando dos binomios de la forma  se multiplican, el producto es . Entonces, por ejemplo, ; observa que los términos −3x y +3x combinados son 0. Ahora para la conexión con racionalizar denominadores: ¿qué si reemplazamos x con ?

Observa los ejemplos siguientes. Así como  se combinan como 0 a la izquierda,  se combinan como 0 a la derecha.

¡Y ahí está! Multiplicar  por  elimina un radical sin sumar otro.

En este ejemplo, a  se le conoce como conjugado, y  y  se les conoce como par conjugado. Para encontrar el conjugado de un binomio que incluye radicales, cambia el signo del segundo término a su opuesto como se muestra en la siguiente tabla.

Una advertencia: este método funcionará para binomios que incluyen una raíz cuadrada, pero no para binomios con raíces mayores que 2. Esto es porque elevar a una raíz con un índice mayor que 2 no elimina la raíz, como se muestra abajo.

no puede seguirse simplificando, porque sus factores primos son . ¡No hay números cúbicos para sacar! Multiplicar  por su conjugado no resulta en una expresión sin radicales.

Identifica el conjugado del denominador.  A)  B)  C)  D)

Cuando te encuentras una fracción que contiene un radical en el denominador, puedes eliminar el radical usando un proceso llamado racionalizar el denominador. Para racionalizar el denominador, necesitas encontrar una cantidad que, cuando se multiplica por el denominador, creará un número racional (sin términos radicales) en el denominador. Cuando el denominador contiene sólo un término, como en , multiplicar la fracción por  va a eliminar el radical del denominador. Cuando del denominador contiene dos términos, como en , identifica el conjugado del denominador, aquí , y multiplica el numerador y el denominador por el conjugado.